题目内容
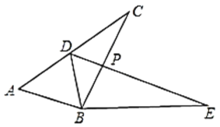
【题目】如图，△ABC中，D是AC上一点，E是BD上一点，∠A=∠CBD=∠DCE．
（1）求证：△ABC∽△CDE；
（2）若BD=3DE，试求
的值．
【答案】（1）证明见解析；（2）
．
【解析】
（1）根据有两个角对应相等的两个三角形相似可得△CDE∽△BDC，同理可得△BDC∽△ABC，由相似的传递性即可得△ABC∽△CDE；
（2）由△CDE∽△BDC，根据相似三角形的性质可得CD2=DE×BD，再根据BD=3DE，可求得CD=
DE，由（1）得：
.
（1）∵∠DCE=∠DBC，∠CDE=∠CDB，
∴△CDE∽△BDC，
同理：△BDC∽△ABC，
∴△ABC∽△CDE；
（2）∵△CDE∽△BDC，
∴CD：BD=DE：DC，
∴CD2=DE×BD，
∵BD=3DE，
∴CD=DE，
由（1）得：.
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
