题目内容
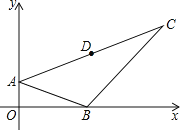
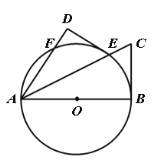
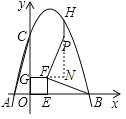
【题目】如图,在平面直角坐标系中,抛物线行![]() 经过点
经过点![]() 和点
和点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 上动点(不与点
上动点(不与点![]() 重合),以
重合),以![]() 为边在
为边在![]() 轴上方作正方形
轴上方作正方形![]() ,接
,接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转90°,得到线段
逆时针旋转90°,得到线段![]() ,过点
,过点![]() 作
作![]() 轴,
轴,![]() 交抛物线于点
交抛物线于点![]() ,设点
,设点![]() .
.

(1)求抛物线的解析式;
(2)若![]() 与
与![]() 相似求
相似求![]() 的值;
的值;
(3)当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)y=-x2+3x+4;(2)a=![]() 或
或![]() ;(3)点P的坐标为(1,4)或(2,4)或(
;(3)点P的坐标为(1,4)或(2,4)或(![]() ,4)
,4)
【解析】
(1)点C(0,4),则c=4,二次函数表达式为:y=-x2+bx+4,将点A的坐标代入上式,即可求解;
(2)△AOC与△FEB相似,则∠FBE=∠ACO或∠CAO,即:tan∠FEB=![]() 或4,即可求解;
或4,即可求解;
(3)证明△PNF≌△BEF(AAS),PH=2,则-4a2+6a+4-4=|2|,即可求解.
解:(1)将点A和点C的坐标代入上式得:0=-1-b+4,
解得:b=3,
故抛物线的表达式为:y=-x2+3x+4;
(2)∵tan∠ACO=![]() =
=![]() ,
,
△AOC与△FEB相似,则∠FBE=∠ACO或∠CAO,
∴tan∠FBE=![]() 或4,
或4,
∵四边形OEFG为正方形,则FE=OE=a,EB=4-a,
则![]() 或
或![]() ,
,
解得:a=![]() 或
或![]() ;
;
(3)令y=-x2+3x+4=0,解得:x=4或-1,故点B(4,0);
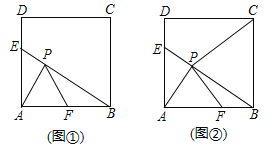
分别延长GF、HP交于点N,
∵∠PFN+∠BFN=90°,∠FPN+∠PFN=90°,
∴∠FPN=∠NFB,
∵GN∥x轴,∴∠FPN=∠NFB=∠FBE,
∵∠PNF=∠BEF=90°,FP=FB,
∴△PNF≌△BEF(AAS),
∴FN=FE=a,PN=EB=4-a,
∴点P(2a,4),点H(2a,-4a2+6a+4),
∵PH=2,
即:-4a2+6a+4-4=±2,
解得:a=1或![]() 或
或![]() 或
或![]() (舍去),
(舍去),
故:点P的坐标为(1,4)或(2,4)或(![]() ,4).
,4).

 阅读快车系列答案
阅读快车系列答案