题目内容
【题目】己知:如图1,⊙O的半径为2, BC是⊙O的弦,点A是⊙O上的一动点。
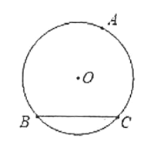
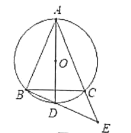
图1 图2
(1)当△ABC的面积最大时,请用尺规作图确定点A位置(尺规作图只保留作图痕迹, 不需要写作法);
(2)如图2,在满足(1)条件下,连接AO并延长交⊙O于点D,连接BD并延长交AC 的延长线于点E,若∠BAC=45° ,求AC2+CE2的值.
【答案】(1)见解析;(2)16.
【解析】
(1)作BC的垂直平分线交优弧BC于A,则点A满足条件;
(2)利用圆周角定理得到∠ACD=90°,根据圆内接四边形的性质得∠CDE=∠BAC=45°,通过判断△DCE为等腰直角三角形得到CE=CD,然后根据勾股定理得到AC2+CE2=AC2+CD2=AD2.
解:(1)如图1,点A为所作;
(2)如图2,连接CD,
∵AD为直径,
∴∠ACD=90°,
∵∠CDE=∠BAC=45°,
∴△DCE为等腰直角三角形,
∴CE=CD,
∴AC2+CE2=AC2+CD2=AD2=42=16.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目