题目内容
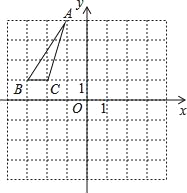
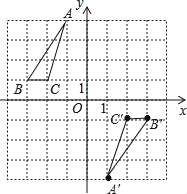
【题目】在如图所示的平面直角坐标系中,△ABC的三个顶点都在小正方形的顶点处,请结合图完成下列各题:
(1)写出tan∠ABC;AB的值;(结果保留根号).
(2)将△ABC绕原点O旋转180°,画出旋转对应的△A′B′C′,并求直线A′C′的函数表达式.
【答案】(1)tan∠ABC=![]() ;AB=
;AB=![]() ;(2)直线A′C′的函数表达式为y=3x﹣7.
;(2)直线A′C′的函数表达式为y=3x﹣7.
【解析】
(1)把∠ABC放到格点直角三角形中,利用正切的定义求它的正切值,然后利用勾股定理计算AB的长;(2)利用关于原点对称的点的坐标特征写出A′、B′、C′点的坐标,然后描点即可得到△A′B′C′,再利用待定系数法求直线A′C′的函数表达式.
(1)tan∠ABC=![]() ;AB=
;AB=![]() ;
;
(2)如图,A′(1,﹣4),B′(3,﹣1),C′(2,﹣1),△A′B′C′为所作;
设直线A′C′的函数表达式为y=kx+b,
把A′(1,﹣4),C′(2,﹣1)代入得![]() ,解得
,解得![]() ,
,
所以直线A′C′的函数表达式为y=3x﹣7.

练习册系列答案
相关题目