Question

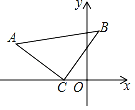
【题目】如图，BC⊥CA，BC=CA，DC⊥CE，DC=CE，直线BD与AE交于点F，与AC交于点G，连接CF.

（1）BD和AE的大小关系是____________，位置关系是____________；请给出证明；

（2）求证：CF平分∠BFE.

Answer 1

【答案】（1）BD=AE，BD⊥AE，证明见解析；（2）证明见解析.

【解析】试题分析: （1）根据垂直的定义得到∠ACB=∠DCE=90°，由角的和差得到∠BCD=∠ACE，即可得到△ACE≌△BCD从而可得到结论；

（2）过C作CH⊥AE于H，CI⊥BF于I，根据全等三角形的性质得到AE=BD，S△ACE=S△BCD，根据三角形的面积公式得到CH=CI，于是得到CF平分∠BFH，推出△ABC是等腰直角三角形，即可得到结论．

试题解析:

（1）BD=AE，BD⊥AE，

证明：∵BC⊥CA，DC⊥CE，

∴∠ACB=∠DCE=90°，

∴∠BCD=∠ACE，

在△BCD与△ACE中，

，

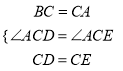∴△ACE≌△BCD；

∴∠CBD=∠CAE，

∵∠BGC=∠AGE，

∴∠AFB=∠ACB=90°，

∴BF⊥AE；

（2）过C作CH⊥AE于H，CI⊥BF于I，

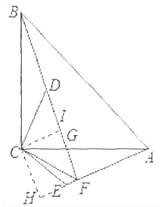
∵△BCD≌△ACE，

∴AE=BD，S△ACE=S△BCD，

∴CH=CI，

∴CF平分∠BFH.

点睛: 本题考查了全等三角形的判定和性质，角平分线的定义，角平分线的性质，等腰直角三角形的性质，正确的作出辅助线是解题的关键．