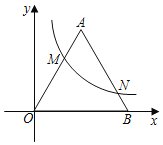题目内容
【题目】如图,在正方形![]() 中,
中,![]() 为线段
为线段![]() 上的动点(不含端点
上的动点(不含端点![]() ),将
),将![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,
,
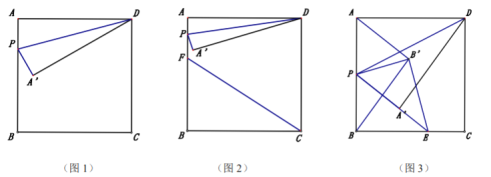
(1)如图1,当![]() ,求
,求![]() 长;
长;
(2)如图2,![]() 为线段
为线段![]() 上的点,当
上的点,当![]() 时,求点
时,求点![]() 由
由![]() 到
到![]() 的运动过程中,线段
的运动过程中,线段![]() 扫过的图形与
扫过的图形与![]() 重叠部分的面积;
重叠部分的面积;
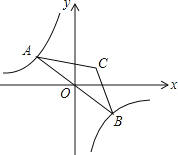
(3)如图3,![]() 在
在![]() 上,连接
上,连接![]() ,将
,将![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,连结
,连结![]() ,问是否存在点
,问是否存在点![]() ,使得
,使得![]() 与
与![]() 相似?若存在,求出
相似?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)重叠部分的面积是
;(2)重叠部分的面积是![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)连接![]() ,根据折叠的性质证
,根据折叠的性质证![]() 是等边三角形即可求解;
是等边三角形即可求解;
(2)因为![]() 在运动的过程中始终都等于DA,即
在运动的过程中始终都等于DA,即![]() 点到D点的距离是定值,故在点
点到D点的距离是定值,故在点![]() 由
由![]() 到
到![]() 的运动过程中,
的运动过程中,![]() 扫过的图形是以D为圆心,以DA为半径的扇形,由此确定
扫过的图形是以D为圆心,以DA为半径的扇形,由此确定![]() 扫过的图形与
扫过的图形与![]() 重合部分是弓形,△
重合部分是弓形,△![]() (
(![]() 恰好在CF上时)是等边三角形,根据扇形及三角形的面积公式求解即可;
恰好在CF上时)是等边三角形,根据扇形及三角形的面积公式求解即可;
(3)先根据![]() 与
与![]() 相似,判定
相似,判定![]() 是直角三角形,分
是直角三角形,分![]() 时、
时、![]() 时两种情况讨论求解即可.
时两种情况讨论求解即可.
(1)如图,连接![]() ,
,
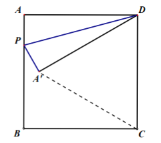
根据折叠的性质可得:
![]()
![]()
![]()
![]() 是等边三角形
是等边三角形
![]()
(2)如图,
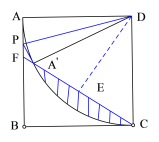
∵四边形ABCD是正方形
∴∠BCD=90°,CD=AD=AB=2
∵![]()
∴∠FCD=60°
![]() 在点
在点![]() 由
由![]() 到
到![]() 的运动过程中,
的运动过程中,![]() 扫过的图形是扇形,
扫过的图形是扇形,
![]() 当
当![]() 与B重合时,点
与B重合时,点![]() 与
与![]() 重合,
重合,
∴![]() 扫过的图形与
扫过的图形与![]() 重合部分是弓形,
重合部分是弓形,
当![]() 运动到如图位置时(
运动到如图位置时(![]() 恰好在CF上时),
恰好在CF上时),![]() =DC
=DC
∴△![]() 是等边三角形,这时
是等边三角形,这时![]()
![]()
过DE⊥CF于E点
![]()
![]() 重叠部分的面积是:
重叠部分的面积是:![]()
(3) 如图,
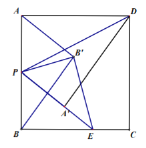
![]() 与
与![]() 关于
关于![]() 对称
对称
![]()
又![]()
![]()
![]()
由折叠可知,![]()
若![]() 与
与![]() 相似,则必
相似,则必![]() 是直角三角形
是直角三角形
①当![]() 时
时
![]()
![]()
![]()
![]()
![]()
②当![]() 时,此时
时,此时![]() 落在
落在![]() 上,
上,
过![]() 作
作![]() ,
,
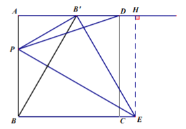
在![]() 中,
中,![]()
![]()
又![]() 在
在![]() 上
上
![]() 与
与![]() 矛盾
矛盾
![]() 综上所述
综上所述![]()

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目