题目内容
【题目】如图1,在□ABCD中,![]() ,
,![]() ,
,![]() ,射线AE平分
,射线AE平分![]() 动点P以
动点P以![]() 的速度沿AD向终点D运动,过点P作
的速度沿AD向终点D运动,过点P作![]() 交AE于点Q,过点P作
交AE于点Q,过点P作![]() ,过点Q作
,过点Q作![]() ,交PM于点
,交PM于点![]() 设点P的运动时间为
设点P的运动时间为![]() ,四边形APMQ与四边形ABCD重叠部分面积为
,四边形APMQ与四边形ABCD重叠部分面积为![]()



![]() ______
______![]() 用含t的代数式表示
用含t的代数式表示![]()
![]() 当点M落在CD上时,求t的值.
当点M落在CD上时,求t的值.
![]() 求S与t之间的函数关系式.
求S与t之间的函数关系式.
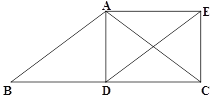
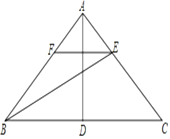
![]() 如图2,连结AM,交PQ于点G,连结AC、BD交于点H,直接写出t为何值时,GH与三角形ABD的一边平行或共线.
如图2,连结AM,交PQ于点G,连结AC、BD交于点H,直接写出t为何值时,GH与三角形ABD的一边平行或共线.
【答案】(1)![]() (2)
(2)![]() (3)
(3)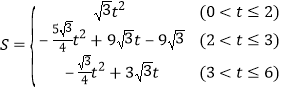
(4)![]() 或
或![]() 或4s时,GH与三角形ABD的一边平行或共线
或4s时,GH与三角形ABD的一边平行或共线
【解析】
(1)由题意得△APQ是直角三角形,∠PAQ=60°,利用正切值即可求得PQ的值;
(2)如图2,由题意可知∠D=60°,四边形APMQ为平行四边形,得∠DPQ=60°,所以△DPM是等边三角形,则DP=MP=AQ=2PA,即6-t=2t,解得t=2;
(3)如图1,3,4,分![]() ,
,![]() ,
,![]() 三种情况讨论,分别计算出三种情况下的重叠部分面积为
三种情况讨论,分别计算出三种情况下的重叠部分面积为![]() 与t的函数关系式即可;
与t的函数关系式即可;
(4)如图5,6,7,分别计算出当![]() ,或GH与BD重合,或
,或GH与BD重合,或![]() 时,三种情况下t的值即可.
时,三种情况下t的值即可.
![]() 如图1中,
如图1中,
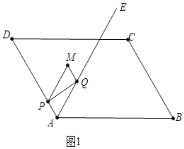
![]() ,AE平分
,AE平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
故答案为![]()
![]() 如图2中,
如图2中,
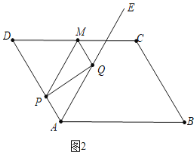
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,四边形APMQ是平行四边形,
,四边形APMQ是平行四边形,
![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 当
当![]() 时,如图1中,重叠部分是平行四边形APMQ,
时,如图1中,重叠部分是平行四边形APMQ,![]() ;
;
![]() 如图3中,当
如图3中,当![]() 时,重叠部分五边形APSTQ,
时,重叠部分五边形APSTQ,
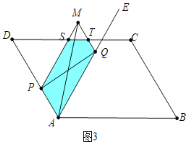
易证△MST为等边三角形,则MT=MP﹣PS=MP﹣DP=2t﹣(6﹣t)=3t﹣6,
故![]() .
.
![]() 如图4中,当
如图4中,当![]() 时,重叠部分是四边形PSTA.
时,重叠部分是四边形PSTA.
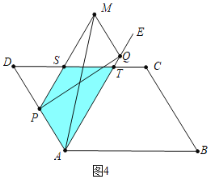
则![]()
综上所述,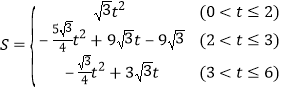 .
.
![]() 如图5中,当
如图5中,当![]() 时,
时,![]() ,
,
![]() 点M在线段CD上,此时
点M在线段CD上,此时![]() .
.
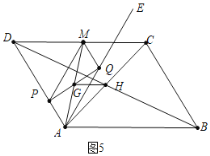
如图6中,当GH与BD重合时,作![]() 交DA的延长线于T.
交DA的延长线于T.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得![]()
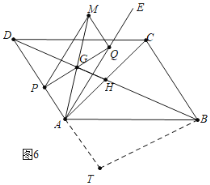
如图7中,当![]() 时,易证B,C,Q共线,
时,易证B,C,Q共线,

可得![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,
![]() ,
,
综上所述,![]() 或
或![]() 或4s时,GH与三角形ABD的一边平行或共线.
或4s时,GH与三角形ABD的一边平行或共线.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案