题目内容
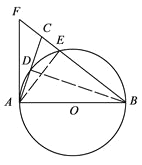
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=![]() ,
, ![]() ,求BE的长.
,求BE的长.
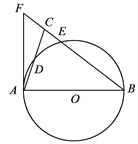
【答案】(1)证明见解析;(2)BE的长为8.
【解析】分析:(1)首先连接BD,由AB为直径,可得∠ADB=90°,又由AF是 O的切线,易证得∠CAF=∠ABD.然后由BA=BC,证得:∠ABC=2∠CAF;
(2)连接AE,利用已知条件分别求出BC,CE的长,由BE=BC-CE计算即可.
本题解析:
(1)证明:连结BD.∵AB是![]() 的直径,∴∠ADB=90°.∴∠DAB+∠DBA=90°.∵AB=AC,∴2∠ABD=∠ABC,AD=
的直径,∴∠ADB=90°.∴∠DAB+∠DBA=90°.∵AB=AC,∴2∠ABD=∠ABC,AD=![]() AC.∵AF为⊙O的切线,∴∠FAB=90°.∴∠FAC+∠CAB=90°.∴∠FAC=∠ABD, ∠ABC=2∠CAF.
AC.∵AF为⊙O的切线,∴∠FAB=90°.∴∠FAC+∠CAB=90°.∴∠FAC=∠ABD, ∠ABC=2∠CAF.
(2)解:连接AE.∴∠AEB=∠AEC=90°.∵sin∠CAF=![]() , ∠ABD=∠CAF=∠CBD=∠CAE∴sin∠ABD=sin∠CAF=
, ∠ABD=∠CAF=∠CBD=∠CAE∴sin∠ABD=sin∠CAF=![]() .∵∠ABD=90°,AC=2
.∵∠ABD=90°,AC=2![]() ,∴AD=
,∴AD=![]() ,AB=
,AB=![]() =10.∵∠AEC=90°,AC=2
=10.∵∠AEC=90°,AC=2![]() ,∴CE=AC·sin∠CAE=2 , ∴BE=BC-CE=10-2=8.
,∴CE=AC·sin∠CAE=2 , ∴BE=BC-CE=10-2=8. 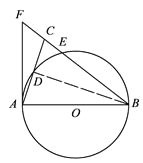

练习册系列答案
相关题目