题目内容
若在正比例函数y=kx中,y随x的增大而减小,那么在反比例函数y=-
中,y随x的增大而
| k | x |
减小
减小
.分析:根据“正比例函数y=kx中,y随x的增大而减小”可以确定k的符号,然后由-k的符号确定反比例函数y=-
所在的象限,以及每一支所在象限的单调性.
| k |
| x |
解答:解:∵在正比例函数y=kx中,y随x的增大而减小,
∴k<0,
∴-k>0,
∴双曲线y=-
位于第一、三象限,且每一支在定义域内是减函数,即y随x的增大而减小;
故答案是:减小.
∴k<0,
∴-k>0,
∴双曲线y=-
| k |
| x |
故答案是:减小.
点评:本题考查了反比例函数的性质、正比例函数的性质.注意y=kx+b和y=
的图象与式子中k的符号之间的关系.
| k |
| x |

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
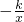 中,y随x的增大而________.
中,y随x的增大而________.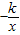 中,y随x的增大而 .
中,y随x的增大而 .