题目内容
【题目】如图,△ABC.
(1)用直尺和圆规作∠A的平分线所在的直线![]() 和边BC的垂直平分线
和边BC的垂直平分线![]() (要求:不写作法,保留画图痕迹);
(要求:不写作法,保留画图痕迹);
(2)设(1)中的直线![]() 和直线
和直线![]() 交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
【答案】(1)作图见解析;(2)证明见解析.
【解析】试题分析:
(1)如图1,用“尺规作图”作出∠ABC的角平分线,再反向延长即可得到![]() ;再用“尺规作图”作出BC的垂直平分线
;再用“尺规作图”作出BC的垂直平分线![]() 即可;
即可;
(2)如图2,连接PB、PC,由题意易证△PBE≌△PCF,从而可得BE=CF.
试题解析:
(1)如图1,图中直线![]() 和直线
和直线![]() 为题中所求直线;
为题中所求直线;
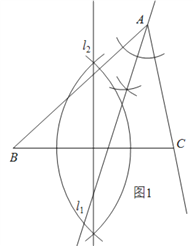
(2)如图2,连接PB、PC,
∵AP平分∠BAC,PE⊥AB于点E,PF⊥AC于点F,
∴PE=PF,∠PEB=∠PFC=90°,
∵![]() 垂直平分BC,点P在
垂直平分BC,点P在![]() 上,
上,
∴PB=PC,
∴△PBE≌△PCF,
∴BE=CF.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目