题目内容
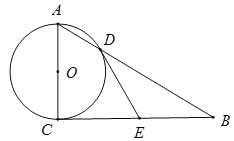
【题目】在△ ABC中,AB = AC

(1)如图 1,如果∠BAD = 30°,AD是BC上的高,AD =AE,则∠EDC =
(2)如图 2,如果∠BAD = 40°,AD是BC上的高,AD = AE,则∠EDC =
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图 3,如果AD不是BC上的高,AD = AE,是否仍有上述关系?如有,请你写出来,并说明理由
【答案】(1)15°;(2)20°;(3)∠BAD=2∠EDC;(4)成立,理由见解析
【解析】
(1)根据等腰三角形三线合一,可知∠DAE=30°,再根据AD=AE,可求∠ADE的度数,从而可知答案;
(2)同理易知答案;
(3)通过(1)(2)题的结论可知∠BAD=2∠EDC,
(4)由于AD=AE,所以∠ADE=∠AED,根据已知容易证得∠BAD=2∠EDC.
解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD=30°
∵AD=AE,
∴![]()
∴∠DEC=90°-∠AD =15°;
(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD=40°
∵AD=AE,
∴![]()
∴∠DEC=90°-∠ADE=20°;
(3)根据前两问可知:∠BAD=2∠EDC
(4)仍成立,理由如下:
∵AD=AE,
∴∠ADE=∠AED
∵∠BAD+∠B=∠ADC,∠ADC=∠ADE+∠EDC
∴∠ADC=∠AED+∠EDC
∵∠AED=∠EDC+∠C
∴∠ADC=(∠EDC+∠C)+∠EDC=2∠EDC+∠C
又∵AB=AC
∴∠B=∠C
∴∠BAD=2∠EDC

练习册系列答案
相关题目