题目内容
【题目】如图所示:抛物线![]() 交坐标轴于
交坐标轴于![]() 、
、![]() 、
、![]() 三点,
三点,![]() 是抛物线的顶点,
是抛物线的顶点,![]() 在对称轴上,
在对称轴上,![]() 在坐标轴上.以下结论:
在坐标轴上.以下结论:
①存在点![]() ,使
,使![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() 的最小值是
的最小值是![]() ;③
;③![]() 的最大值是
的最大值是![]() ;④若
;④若![]() 与
与![]() 相似,则
相似,则![]() 的坐标恰有两个.
的坐标恰有两个.
其中正确的是________(只填序号)
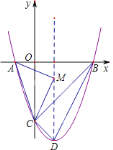
【答案】①②③
【解析】
先根据抛物线的解析式确定点![]() 的坐标为
的坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,对称轴为直线
,对称轴为直线![]() ,
,![]() 点坐标为
点坐标为![]() ;由于
;由于![]() 为等腰直角三角形,易得
为等腰直角三角形,易得![]() ,则
,则![]() ,可得到
,可得到![]() 点坐标为
点坐标为![]() ;由于点
;由于点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,根据两点之间线段最短得到当
对称,根据两点之间线段最短得到当![]() 点在
点在![]() 的位置时,
的位置时,![]() 有最小值,最小值为
有最小值,最小值为![]() 的长,运用勾股定理可计算
的长,运用勾股定理可计算![]() ;由于三角形任意两边之差小于第三边,则当
;由于三角形任意两边之差小于第三边,则当![]() 点在
点在![]() 的位置时,
的位置时,![]() 有最大值,最大值为
有最大值,最大值为![]() 的长,再根据勾股定理可计算出
的长,再根据勾股定理可计算出![]() ;根据勾股定理的逆定理可得到
;根据勾股定理的逆定理可得到![]() ,若
,若![]() 与
与![]() 相似,则
相似,则![]() 为直角三角形,当
为直角三角形,当![]() 时,根据
时,根据![]() ,可得到
,可得到![]() ,则
,则![]() 满足条件;当
满足条件;当![]() 时,由于
时,由于![]() ,可得到
,可得到![]() 满足条件;当
满足条件;当![]() 时,由于
时,由于![]() 得到
得到![]() ,则有
,则有![]() 满足条件.
满足条件.
令![]() ,则
,则![]() ,解得
,解得![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,
![]()
![]() ,
,
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
(1)设![]() 点坐标为
点坐标为![]() ,作
,作![]() 直线
直线![]() ,直线
,直线![]() 与
与![]() 轴交于
轴交于![]() 点,如图,
点,如图,
当![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() ,
,
![]()
![]() ,
,
![]()
![]() 点坐标为
点坐标为![]() ,所以①正确;
,所以①正确;
(2)点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,
对称,![]() 与直线
与直线![]() 的交点为
的交点为![]() ,
,
当![]() 点在
点在![]() 的位置时,
的位置时,![]() 有最小值,最小值为
有最小值,最小值为![]() 的长,即
的长,即![]() ,所以②正确;
,所以②正确;
(3)延长![]() 交直线
交直线![]() 于
于![]() ,
,
当![]() 点在
点在![]() 的位置时,
的位置时,![]() 有最大值,最大值为
有最大值,最大值为![]() 的长,即
的长,即![]() ,所以③正确;
,所以③正确;
(3)![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
点![]() 点在原点,即
点在原点,即![]() 的位置时,
的位置时,![]() ,
,
![]()
![]() ,
,
![]()
![]() 满足条件,
满足条件,
当![]() 时,
时,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() 满足条件;
满足条件;
当![]() 时,
时,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() 满足条件,所以④错误.
满足条件,所以④错误.
故答案为:①②③.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目