题目内容
【题目】已知△ABC中,AB=AC,过B点作射线BE,过C点作射线CF,使∠ABE=∠ACF,且射线BE,CF交于点D,过A点作AM⊥BD于M.
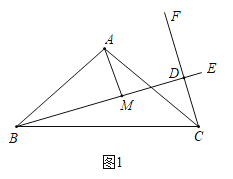
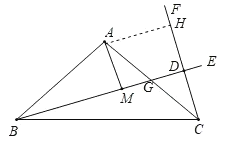
⑴如图1所示,若BE⊥CF,AB=6,∠ABE=30°,求CD;
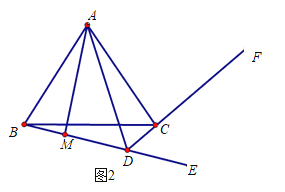
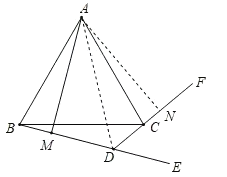
⑵如图2所示,求证:BM=DM﹣DC.
【答案】(1)3![]() -3 (2)见解析;
-3 (2)见解析;
【解析】
(1)设AC与BE交于G,过A作AH⊥CF于H,根据矩形的性质得到DH=AM,解直角三角形得到AM=2,BM=2![]() ,根据全等三角形的性质得到=BM=2
,根据全等三角形的性质得到=BM=2![]() ,于是得到结论;
,于是得到结论;
(2)作AN⊥CF于N,连接AD,先通过△AMB≌△ANC求得BM=CN=DNDC,AM=AN,然后通过证明RT△AMD≌RT△AND得出DM=DN,即可求得BM=DMDC.
(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
∵![]() ,
,
∴![]() .
.
在![]() 与
与![]() 中,
中,
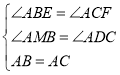
∴![]() ≌
≌![]() (
(![]() ),
),
∴![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,
![]() ,
,
∴![]() ≌
≌![]() (HL),
(HL),
∴![]() ,
,
∴![]() .
.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目