题目内容
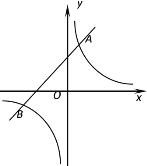
【题目】如图,抛物线y=mx2+2mx﹣3与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点C,且x2﹣x1=4.
(1)求抛物线的解析式;
(2)求抛物线的对称轴上存在一点P,使PA+PC的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标.
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.
【答案】(1)y=x2+2x3;(2)P的坐标为:(-1,-2);(3)①点M的坐标为(-1,-4)时,△AMB的面积最大,最大值为8;②点M的坐标为(-![]() ,-
,-![]() )时,四边形AMCB的面积最大,最大值为
)时,四边形AMCB的面积最大,最大值为![]() .
.
【解析】
(1)由![]() ,与
,与![]() ,联立方程组求出
,联立方程组求出![]() ,再将A或B点坐标代入抛物线即可求解;
,再将A或B点坐标代入抛物线即可求解;
(2)根据两点之间线段最短,连接AC交抛物线的对称轴于点P,则PA+PC的值最小,求出直线PC的解析式,与对称轴的交点即为所求;
(3)
(1)由题意得 ,解得
,解得 ,∴B点坐标为(1,0),
,∴B点坐标为(1,0),
将(1,0)代入![]() 得,
得,![]() ,∴
,∴![]()
抛物线的表达式为:![]() .
.
(2)如图1,连接AC交抛物线的对称轴于点P,则PA+PC的值最小,
当y=0时,![]() ,解得:x=-3或x=1.
,解得:x=-3或x=1.
∵A在B的左侧,∴A(-3,0),B(1,0),设直线AC的解析式为:y=kx+b,则
![]() ,解得:
,解得:![]() ,
,
∴直线AC的解析式为:![]() ,
,
∵抛物线对称轴![]()
当![]() 时,
时,![]() ,∴点P的坐标为:(-1,-2)
,∴点P的坐标为:(-1,-2)

(3)如图2,点M是抛物线上的一动点,且在第三象限,∴-3<x<0;
①设点M的坐标为: ![]() ,
,
∵点M在第三象限,∴M到x轴的距离为![]()
∵![]() ,∴S△AMB=
,∴S△AMB=![]() .
.
∴当x=-1时,即点M的坐标为(-1,-4)时,△AMB的面积最大,最大值为8;

②设点M的坐标为:![]() ,如图3,过点M作MD⊥AB于D,则
,如图3,过点M作MD⊥AB于D,则
![]() ,
,![]() ,
,![]()
∴S四边形ABCM=S△OBC+S△ADM+S梯形OCMD
=![]()
=![]()
=![]()
= ,∴当
,∴当![]() 时,
时, ,
,
即当点M的坐标为![]() 时,四边形AMCB的面积最大,最大值为
时,四边形AMCB的面积最大,最大值为![]() .
.