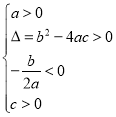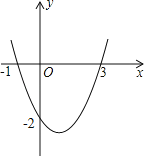题目内容
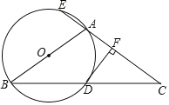
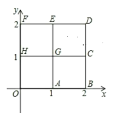
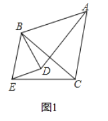
【题目】已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE.
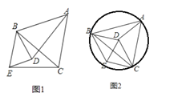
(1)求证:△ABD≌△CBE;
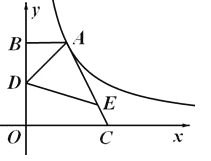
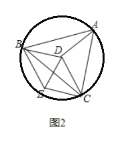
(2)如图2,当点D是△ABC的外接圆圆心时:
①请判断四边形BDCE的形状,并证明你的结论
②当∠ABC为多少度时,点E在圆D上?请说明理由.
【答案】(1)见解析;(2)①四边形BDCE是菱形,证明见解析;②60°,理由见解析.
【解析】
(1)由∠ABC=∠DBE可知∠ABC+∠CBD=∠DBE+∠CBD,即∠ABD=∠CBE,根据SAS可证△ABD≌△CBE;
(2)①根据点D是△ABC的外接圆圆心可知DB=DA=DC,由(1)中全等得AD=CE ,进而得到DB=DC=BE=CE,根据菱形判定定理可知四边形BDCE是菱形;
②点E在圆D上,则DE=BD,根据BD=BE,则△BDE为等边三角形,即可知∠EBD为60°,根据题意∠ABC=∠DBE,即可求得∠ABC的度数.
(1) 
∵∠ABC=∠DBE
∴∠ABC+∠CBD=∠DBE+∠CBD
即∠ABD=∠CBE
∵BA=BC,BD=BE
∴△ABD≌△CBE(SAS)
(2)①四边形BDCE是菱形;理由如下:
点D是△ABC的外接圆圆心,∴DB=DA=DC
∵△ABD≌△CBE ∴AD=CE ∴DB=DC=BE=CE
∴四边形BDCE是菱形
②当∠ABC为60°时,点E在圆D上,
证明:∵点E在圆D上,∴DE=BD,
∵BD=BE
∴△BDE为等边三角形
∴∠EBD=60°,
∴∠ABC=∠DBE=60°
∴当∠ABC为60°时,点E在圆D上

 名校通行证有效作业系列答案
名校通行证有效作业系列答案【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
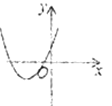
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
____________ |
|
|
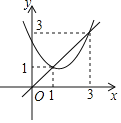
方程有两个不相等的正实根 | ____________ | ____________ |
(1)参考小明的做法,把上述表格补充完整;
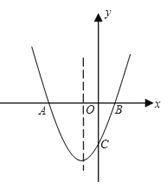
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.