题目内容
【题目】如图，在直角坐标系中，矩形OABC的顶点A、B在双曲线y＝
（ x＞0）上，BC与x轴交于点D．若点A的坐标为（2，4），则点D的坐标为（ ）
A.（
，0）B.（
，0）C.（
，0）D.（
，0）
【答案】B
【解析】
由矩形OABC的顶点A、B在双曲线y＝
（ x＞0）上，BC与x轴交于点D．若点A的坐标为（2，4），利用待定系数法即可求得反比例函数与直线OA的解析式，又由OA⊥AB，可得直线AB的系数为
，继而可求得直线AB的解析式，将直线AB与反比例函数联立，即可求得点B的坐标，设直线BD的解析式为y＝2x＋c，代入求出解析式，再求出直线和x轴的交点坐标即可．
∵矩形OABC的顶点A、B在双曲线y＝（ x＞0）上，点A的坐标为（2，4），
∴4＝
，
解得：k＝8，
∴双曲线的解析式为：y＝
，直线OA的解析式为：y＝2x，
∵OA⊥AB，
∴设直线AB的解析式为：y＝x＋b，
∴4＝×2＋b，
解得：b＝5，
∴直线AB的解析式为：y＝x＋5，
将直线AB与反比例函数联立得出：
，
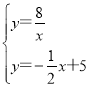解得：
或
，
∴点B（8，1），
∵四边形AOCB是矩形，
∴AO∥BD，
∵直线OA的解析式为y＝2x，
∴设直线BD的解析式为y＝2x＋c，
把B的坐标代入得：1＝16＋c，
解得c＝15，
即y＝2x15，
当y＝0时，x＝
，
即D的坐标为（，0），
故选：B．
练习册系列答案
相关题目
