题目内容
【题目】已知四边形ABCD中,∠ABC+∠ADC=180,连接AC,BD.
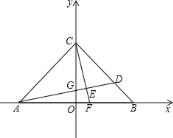
(1)如图1,当∠ACD=∠CAD=45时,求∠CBD的度数;
(2)如图2,当∠ACD=∠CAD=60时,求证:AB+BC=BD;
(3)如图3,在(2)的条件下,过点C作CK⊥BD于点K,在AB的延长线上取点F,使∠FCG=60,过点F作FH⊥BD于点H,BD=8,AB=5,GK=![]() ,求BH的长。
,求BH的长。

【答案】(1)45°
(2)见解析
(3)![]()
【解析】
(1)根据已知条件得到A,B,C,D四点共圆,根据圆周角定理即可得到结论;
(2)在BD截取BE=AB,连接CE,根据圆周角定理得到∠ABD=∠ACD=60°,推出△ABE是等边三角形,△ACD是等边三角形,根据全等三角形的性质即可得到结论;
(3)根据圆周角定理得到∠CBD=∠ABC=∠CAD=60°,解直角三角形得到BK=![]() ,
,![]() ,CK=
,CK=![]() ,DK=
,DK=![]() ,由勾股定理得到CD=7,求得AC=CD=7,根据相似三角形的性质得到AF=
,由勾股定理得到CD=7,求得AC=CD=7,根据相似三角形的性质得到AF=![]() ,BF=
,BF=![]() ,解直角三角形即可得到结论.
,解直角三角形即可得到结论.
(1) ∵∠ABC+∠ADC=180,
∴A,B,C,D四点共圆,
∵∠ACD=∠CAD=45,
∴∠CBD=∠CAD=45;
(2) 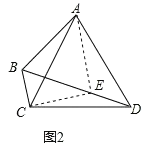 在BD截取BE=AB,连接CE,
在BD截取BE=AB,连接CE,
∵∠ABC+∠ADC=180,
∴A,B,C,D四点共圆,
∴∠ABD=∠ACD=60,
∴△ABE是等边三角形,
∴AB=BE=AE,
∵∠ACD=∠CAD=60,
∴△ACD是等边三角形,
∴AC=AD,∠CAD=∠BAE=60,
∴∠BAC=∠DAE,
在△ABC与△ADE中,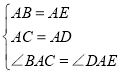
∴△ABC≌△AED,
∴BC=DE,
∵BD=BE+DE,
∴BD=BC+AB;
(3)∵BD=8,AB=5,
∴BC=3,
∵A,B,C,D四点共圆,
∴∠CBD=∠ABC=∠CAD=60,
∵CK⊥BD,
∴BK=![]() BC=
BC=![]() ,CK=
,CK=![]() ,
,
∴DK=![]() ,
,
∴CD=![]() =7
=7
∴AC=CD=7,
∵∠FCG=60,
∴∠FCG=∠CBD,
∵A,B,C,D四点共圆,
∴∠BAC=∠CDB,
∴△AFC∽△DCB,
∴![]() ,
,
∴AF=![]() ,
,
∴BF=![]() ,
,
∵∠FBH=∠ABD=60,
∵FH⊥BD,
∴BH=![]() BF=
BF=![]() .
.