题目内容
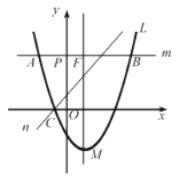
【题目】如图，抛物线
（
，
为常数且
）经过点
，顶点为
，经过点
的直线
与
轴平行，且与
交于点
，
（在的右侧），与的对称轴交于点
，直线
经过点
．
（1）用表示及点的坐标；
（2）
的值是否是定值？若是，请求出这个定值；若不是，请说明理由；
（3）当直线
经过点时，求的值及点，的坐标；
（4）当
时，设
的外心为点
，则
①求点的坐标；
②若点
在的对称轴上，其纵坐标为
，且满足
，直接写出的取值范围．
【答案】（1）
，
；（2）是，定值为2；（3）
，
，
；（4）①
；②
或
．
【解析】
（1）首先根据题意将点C坐标代入抛物线解析式求出，然后将抛物线解析式化为顶点式，最后将代入，由此即可得出点M的坐标；
（2）首先利用抛物线的对称性得出
，然后进一步根据点M的坐标得出PF=1，最后通过
进一步化简变形求解即可；
（3）根据“直线
经过点
”列出方程
，然后结合抛物线的开口方向所判断出的
将原方程化简为
，由此解出方程，结合题意分别表示出A、B两点的坐标，最后再代入直线的解析式求出
的值，由此进一步求解即可得出答案；
（4）①根据抛物线的轴对称性可知，
的对称轴
就是
的垂直平分线，由此得出
的外心
就在直线上，则有
，据此进一步设N点坐标为(
，
)，再结合点A、C的坐标建立方程，求出的值，从而即可得出点N的坐标；②结合题意可得点Q(1，
)，然后利用C、N两点的坐标得出
半径
，由此进一步得出
，最后根据题意进一步分析讨论即可.
（1）把点C(
，0)代入抛物线，得：
，
∴．
∴抛物线L解析式为：
，
顶点M坐标为(1，
)；
（2）是定值，
根据图像，由抛物线的轴对称性，可知，
又∵抛物线L的对称轴为，故
，
∴
；
（3）当直线经过点时，有，
化简得，
，
∵根据抛物线开口向上可知，
∴，
解得：
，
，
∵B在
的右侧，对称轴为，
∴B点坐标为：(4，
)，A点坐标为(
，)，
把点代入直线，得
，解得，
∴A点坐标为(，
)，B点坐标为：(4，)；
（4）
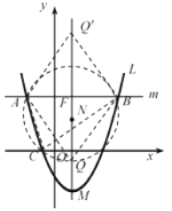
①根据抛物线的轴对称性可知，的对称轴就是的垂直平分线，
故的外心就在直线上，则有．
∴设N点坐标为(，)，由（3）可知A点坐标为(，)，及C点坐标为(，
)，
∴
，
即
，解得
，
∴N点坐标为(，
)；
②或．
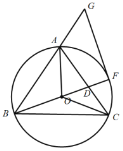
如图，对于点Q(1，)，若
，
根据同弧所对的圆周角相等，可得点
为与的交点，
∵N点坐标为(，)，C点坐标为(，)，
∴的半径为，
则；
设点关于直线的对称点为
，若
，
则
．
综上，若点满足
，则有或．
