��Ŀ����
����Ŀ�������½�һ��Բ���˹�����Ϊ�����ú��İ뾶��С�ܺ�С���غ���ѡȡA��B��C����ľ����ʹ��A��B֮��ľ�����A��C֮��ľ�����ȣ������BC��Ϊ120�ף�A��BC�ľ���Ϊ4�ף���ͼ��ʾ�� 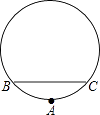
��1���������������ú��İ뾶��
��2�������Բ��������ȡһ��P������һ������B��C��P����������������ţ��ҡ�BCPΪֱ�������Σ��ʣ�������P������м���������ҵ���
���𰸡�
��1���⣺��Բ��Ϊ��O������OB��OA��OA���߶�BC�ڵ�D��
��AB=AC��
�� ![]() =
= ![]() ��
��
��OA��BC��
��BD=DC= ![]() BC=60
BC=60
��DA=4�ף�
��Rt��BDO��OB2=OD2+BD2��
��OB=x�ף�
��x2=��x��4��2+602��
���x=452��
���˹����İ뾶Ϊ452��
��2���⣺������P�������2��������B���C��BC�Ĵ��߽�Բ��һ�㣬�˵㼴ΪP�㣮
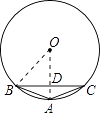
����������1����Բ��Ϊ��O������OB��OA��AB=AC���ó� ![]() =
= ![]() ���ٸ��ݵ��ҶԵȻ����ó���A�ǻ�BC���е㣮��ϴ������������ۣ�֪OA��ֱƽ���ң���Բ�İ뾶����ϴ����������ɶ����г����ڰ뾶�ķ��̣��������Բ�İ뾶����2�����ݴ�ֱ�Ķ��弴�ɵõ����ۣ�
���ٸ��ݵ��ҶԵȻ����ó���A�ǻ�BC���е㣮��ϴ������������ۣ�֪OA��ֱƽ���ң���Բ�İ뾶����ϴ����������ɶ����г����ڰ뾶�ķ��̣��������Բ�İ뾶����2�����ݴ�ֱ�Ķ��弴�ɵõ����ۣ�
�����㾫����������Ŀ����֪���������ô������������۵����֪ʶ���Եõ�����Ĵ𰸣���Ҫ��������1��A��ƽ���ң�����ֱ������ֱ����ֱ���ң�����ƽ�������Ե�������B���ҵĴ�ֱƽ���߾���Բ�ģ�����ƽ�������Ե�������C��ƽ�������Ե�һ������ֱ������ֱƽ���ң�����ƽ�������Ե���һ����������2 ��Բ������ƽ�������еĻ���ȣ�

����Ŀ��Ϊ�˽�ij��������ɫ���С���ʽ�������ijУ��ѧ��ȤС�����ʾ��������ʽ�����������ij�в��ֳ����������Ҫ���з�ʽ�������ʾ����������ֻ���������������ѡ��һ�ࣩ���������������Ƴ����²�������ͳ��ͼ��
���� | A | B | C | D | E |
���з�ʽ | �������� | ���� | ������ | ��ʿ | ˽�ҳ� |

����������Ϣ���ش��������⣺
��1�����뱾���ʾ������������ �ˣ�����ѡ��B��������� �ˣ�
��2��������ͳ��ͼ�У���A���Ӧ����Բ�ĽǦ��Ķ���������ȫ����ͳ��ͼ��
��3������Լ��12���˳��У�����A��B��C��������з�ʽ����Ϊ����ɫ���С���ʽ������Ƹ��С���ɫ���С���ʽ��������