题目内容
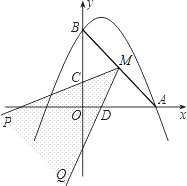
已知:如图,在平面直角坐标系中,半径为2
的⊙O′与y轴交于A、B两点,与直线 OC相切于点C,∠BOC=45°,BC⊥OC,垂足为C.
OC相切于点C,∠BOC=45°,BC⊥OC,垂足为C.
(1)判断△ABC的形状;
(2)在
上取一点D,连接DA、DB、DC,DA交BC于点E.求证:BD•CD=AD•ED;
(3)延长BC交x轴于点G,求经过O、C、G三点的二次函数的解析式.
| 2 |
 OC相切于点C,∠BOC=45°,BC⊥OC,垂足为C.
OC相切于点C,∠BOC=45°,BC⊥OC,垂足为C.(1)判断△ABC的形状;
(2)在
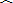 |
| BC |
(3)延长BC交x轴于点G,求经过O、C、G三点的二次函数的解析式.
(1)∵OC与⊙O'相切
∴O'C⊥OC
又∵BC⊥OC
∴O'在BC上,即BC为⊙O'的直径
∴∠CAB=90°
∴CA⊥BA
∵∠BOC=45°
∴△BOC为等腰直角三角形
∴A为OB的中点,CD=
OB=AB
∴△ABC是等腰直角三角形.
(2)证明:∵AC=AB
∴
=
.
∴∠ADC=∠ADB
又∵∠CAD=∠CBD
∴△ADC∽△BDE
∴
=
,
即BD•CD=AD•ED.
(3)在Rt△BOC中
∵⊙O′的半径为2
∴BC=4
∵∠BOC=45°
∴OB=
•BC=8,CA=OA=AB=
OB=4
∵CA∥x轴,
∴C点坐标为(-4,-4)
∴BC=CG
∴AC为△BGO的中位线
∴OG=2AC=8
∴G点坐标为(-8,0)
设过O、C、G三点的二次函数为y=ax2+bx+c,
由已知,函数图象过(0,0),(-4,-4),(-8,0)三点,得
解这个方程组,得
a=
,b=2,c=0
因此,所求二次函数是y=
x2+2x.
∴O'C⊥OC
又∵BC⊥OC
∴O'在BC上,即BC为⊙O'的直径
∴∠CAB=90°
∴CA⊥BA
∵∠BOC=45°
∴△BOC为等腰直角三角形
∴A为OB的中点,CD=
| 1 |
| 2 |
∴△ABC是等腰直角三角形.
(2)证明:∵AC=AB
∴
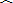 |
| AC |
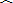 |
| AB |
∴∠ADC=∠ADB
又∵∠CAD=∠CBD
∴△ADC∽△BDE
∴
| AD |
| BD |
| DC |
| DE |
即BD•CD=AD•ED.
(3)在Rt△BOC中
∵⊙O′的半径为2
| 2 |
∴BC=4
| 2 |
∵∠BOC=45°
∴OB=
| 2 |
| 1 |
| 2 |
∵CA∥x轴,
∴C点坐标为(-4,-4)
∴BC=CG
∴AC为△BGO的中位线
∴OG=2AC=8
∴G点坐标为(-8,0)
设过O、C、G三点的二次函数为y=ax2+bx+c,
由已知,函数图象过(0,0),(-4,-4),(-8,0)三点,得
|
解这个方程组,得
a=
| 1 |
| 4 |
因此,所求二次函数是y=
| 1 |
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




 ?
?