Question

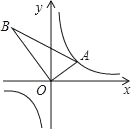
【题目】如图，△AOB是直角三角形，∠AOB＝90°，OB＝2OA，点A在反比例函数y＝的图象上．若点B在反比例函数y＝的图象上，则k的值为_____．

Answer 1

【答案】﹣8

【解析】

要求函数的解析式只要求出B点的坐标就可以，过点A，B作AC⊥x轴，BD⊥x轴，分别于C，D．根据条件得到△ACO∽△ODB，得到：=2，然后用待定系数法即可．

过点A，B作AC⊥x轴，BD⊥x轴，分别于C，D．

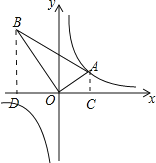
设点A的坐标是（m，n），则AC=n，OC=m．

∵∠AOB=90°，

∴∠AOC+∠BOD=90°．

∵∠DBO+∠BOD=90°，

∴∠DBO=∠AOC．

∵∠BDO=∠ACO=90°，

∴△BDO∽△OCA．

∴,

∵OB=2OA，

∴BD=2m，OD=2n．

因为点A在反比例函数y=的图象上，

∴mn=2．

∵点B在反比例函数y=的图象上，

∴B点的坐标是（-2n，2m）．

∴k=-2n2m=-4mn=-8．

故答案为：-8．