题目内容
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1厘米,AB=3厘米,BC=5厘米,动点P从点B出发以1厘米/秒的速度沿BC方向运动,动点Q从点C出发以2厘米/秒的速度沿CD方向运动,P,Q两点同时出发,当点Q到达点D时停止运动,点P也随之停止,设运动时间为t秒(t>0).
(1)求线段CD的长。
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
(3)伴随P,Q两点的运动,线段PQ的垂直平分线为l.
①t为何值时,l经过点C?
②求当l经过点D时t的值,并求出此时刻线段PQ的长。
【答案】
(1)
解:如图1,作DE⊥BC于E,
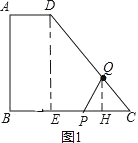
∵AD∥BC,∠A=90°,
∴四边形ABED为矩形,
∴BE=AD=1,DE=AB=3,
∴EC=BC﹣BE=4,
在Rt△DEC中,DE2+EC2=DC2,
∴CD=![]() =5厘米;
=5厘米;
(2)
解:∵点P的速度为1厘米/秒,点Q的速度为2厘米/秒,运动时间为t秒,
∴BP=t厘米,PC=(5﹣t)厘米,CQ=2t厘米,QD=(5﹣2t)厘米,
且0<t≤2.5,
作QH⊥BC于点H,
∴DE∥QH,
∴∠DEC=∠QHC,
∵∠C=∠C,
∴△DEC∽△QHC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴QH=![]() t,
t,
∴![]() =
=![]() =
=![]() (5-t)
(5-t)![]() =-
=-![]() ,
,
S四边形ABCD=![]() (AD+BC)
(AD+BC)![]() AB=
AB=![]() (1+5)×3=9,
(1+5)×3=9,
分两种情况讨论:
①当S△PQC:S四边形ABCD=1:3时,-![]() ,
,
即t2﹣5t+5=0,
解得:t1=![]() ,t2=
,t2=![]() (舍去);
(舍去);
②S△PQC:S四边形ABCD=2:3时,-![]() ,
,
即t2﹣5t+10=0,
∵△<0,
∴方程无解,
∴当t为![]() 秒时,线段PQ将四边形ABCD的面积分为1:2两部分;
秒时,线段PQ将四边形ABCD的面积分为1:2两部分;
(3)
解:如图2,

①当PQ的垂直平分线l经过点C时,可知PC=QC,
∴5﹣t=2t,
∴3t=5,
∴t=![]() ,
,
∴当t=![]() 秒时,直线l经过点C
秒时,直线l经过点C
②如图3,
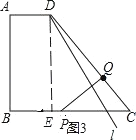
当PQ的垂直平分线l经过点D时,
可知DQ=DP,
连接DP,则在Rt△DEP中,DP2=DE2+EP2,
∴DQ2=DE2+EP2,
∴(5﹣2t)2=32+(t﹣1)2,
∴t1=1,t2=5(舍去),
∴BP=1厘米,
∴当t=1秒时,直线l经过点D,此时点P与点E重合;
如图4,连接FQ,
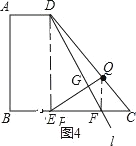
∵直线l是△DPQ的对称轴,
∴△DEF≌△DQF,∠DQF=90°,EF=QF,
设EF=x厘米,则QF=x厘米,FC=(4﹣x)厘米,
在Rt△FQC中,FQ2+QC2=FC2,
x2+22=(4﹣x)2,
∴x=![]() ,
,
∴EF=![]() 厘米,
厘米,
在Rt△DEF中,DE2+EF2=DF2,
∴32+(![]() )2=DF2,
)2=DF2,
∴DF=![]() 厘米,
厘米,
在Rt△DEF中,EG⊥DF,
∴![]() =
=![]()
![]() =
=![]()
![]() ,
,
∴EG=![]() ,
,
∴EG=![]() 厘米,
厘米,
∴PQ=2EG=![]() 厘米.
厘米.
【解析】(1)作DE⊥BC于E,根据勾股定理即可求解;
(2)线段PQ将四边形ABCD的面积分为1:2两部分,分两种情况进行求解;
(3)①当PQ的垂直平分线经过点C进行分析解答;
②当PQ的垂直平分线l经过点D时进行分析解答.
此题考查了梯形中动点问题,用到了勾股定理,垂直平分线定理等,注意分情况讨论。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案