题目内容
【题目】如图1,E为矩形ABCD边AD上的一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是2cm/s.若P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t的函数关系图象如图2,则下列结论错误的是( )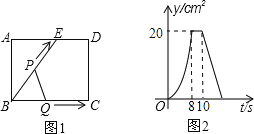
A.AE=12cm
B.sin∠EBC=![]()
C.当0<t≤8时,y=![]() t2
t2
D.当t=9s时,△PBQ是等腰三角形
【答案】D
【解析】A、分析函数图象可知,BC=16cm,ED=4cm,故AE=AD﹣ED=BC﹣ED=16﹣4=12cm,故①正确;
B、如答图1所示,连接EC,过点E作EF⊥BC于点F,
由函数图象可知,BC=BE=16cm,ED=4cm,则BF=12cm,
由勾股定理得,EF=4![]() ,
,
∴sin∠EBC=![]() =
=![]()
![]() ,故②正确;
,故②正确;
C、如答图2所示,过点P作PG⊥BQ于点G,
∵BQ=BP=2t,
∴y=S△BPQ=![]() BQPG=
BQPG=![]() BQBPsin∠EBC=
BQBPsin∠EBC=![]() ×2t2t
×2t2t![]() =
=![]() t2 .
t2 .
故③正确;
D、当t=9s时,点Q与点C重合,点P运动到ED的中点,设为N,如答图3所示,连接NB,NC.
此时AN=14,ND=2,由勾股定理求得:NB=![]() ,NC=
,NC=![]() ,
,
∵BC=16,
∴△BCN不是等腰三角形,即此时△PBQ不是等腰三角形.
故④错误;
故选:D.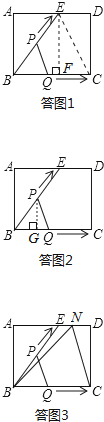

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数 ![]() (单位:分)及方差s2如表所示:
(单位:分)及方差s2如表所示:
甲 | 乙 | 丙 | 丁 | |
| 7 | 8 | 8 | 7 |
s2 | 1 | 1.2 | 1 | 1.8 |
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
A.甲
B.乙
C.丙
D.丁


