题目内容
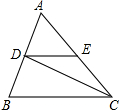
如图，在Rt△ABC中，∠C="90" o，AC=BC，BE平分∠ABC， ED⊥AB交AB于D，若AB=2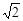
㎝，则△ADE的周长是 。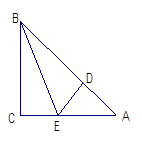
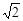㎝，则△ADE的周长是 。
试题分析：从已知条件进行思考，根据角平分线性质得CE=DE，求证△BCE≌△BDE，得出BC=BD，再利用求出BC，进一步求出AD，然后求AD+DE+AE．即为△ADE的周长．
∵BE平分∠ABC，ED⊥AB于点D，∠C=90°，
∴CE=DE，
∵BE为公共边，
∴△BCE≌△BDE，
∴BC=BD，
∵∠C=90°，AB=
cm，∴BC=AC=2，
∴AD=AB-BD=
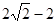，∴AD+DE+AE=AD+CE+AE=AD+AC=
点评：利用角平分线性质将相等的线段进行转化，是求三角形周长的关键．
练习册系列答案
相关题目
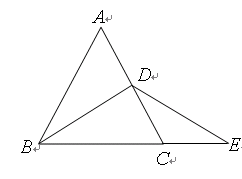
，则 BC = ．
，∠B=
，BC=4，则AB=_____.
、
、
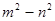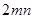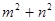
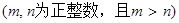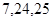；⑵
； ⑶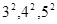
；⑷
；⑸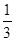
、
、
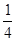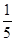；其中可以构成直角三角形的有（ ）组。
