题目内容
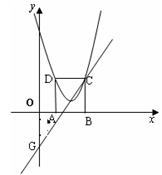
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=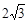 ,直线y=
,直线y=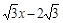 经过点C,交y轴于点G,且∠AGO=30°。
经过点C,交y轴于点G,且∠AGO=30°。
(1)点C、D的坐标
(2)求顶点在直线y=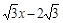 上且经过点C、D的抛物线的解析式;
上且经过点C、D的抛物线的解析式;
(3)将(2)中的抛物线沿直线y=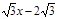 平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
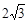 ,直线y=
,直线y=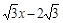 经过点C,交y轴于点G,且∠AGO=30°。
经过点C,交y轴于点G,且∠AGO=30°。
(1)点C、D的坐标
(2)求顶点在直线y=
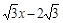 上且经过点C、D的抛物线的解析式;
上且经过点C、D的抛物线的解析式;(3)将(2)中的抛物线沿直线y=
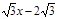 平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。(1)C(4,
 ),D(1,
),D(1, );
);(2)
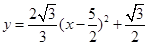 ;
;(3)见解析。
(1)根据题意可得点C的纵坐标为3,代入直线解析式可得出点C的横坐标,继而也可得出点D的坐标;
(2)由题意可得点C和点D关于抛物线的对称轴对称,从而得出抛物线的对称轴为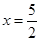 ,再由抛物线的顶点在直线
,再由抛物线的顶点在直线 ,可得出顶点坐标为(
,可得出顶点坐标为(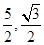 ),设出顶点式,代入点C的坐标即可得出答案.
),设出顶点式,代入点C的坐标即可得出答案.
(3)分EF=EG、GF=EG、GF=EF三种情况分析。
解:(1)C(4, ),D(1,
),D(1, );
);
(2)顶点(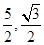 ),解析式
),解析式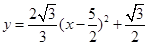 ;
;
(3)EF=EG
GF=EG
GF=EF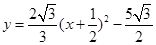
(2)由题意可得点C和点D关于抛物线的对称轴对称,从而得出抛物线的对称轴为
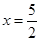 ,再由抛物线的顶点在直线
,再由抛物线的顶点在直线 ,可得出顶点坐标为(
,可得出顶点坐标为(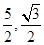 ),设出顶点式,代入点C的坐标即可得出答案.
),设出顶点式,代入点C的坐标即可得出答案.(3)分EF=EG、GF=EG、GF=EF三种情况分析。
解:(1)C(4,
 ),D(1,
),D(1, );
);(2)顶点(
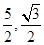 ),解析式
),解析式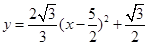 ;
;(3)EF=EG

GF=EG

GF=EF
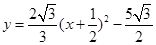

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
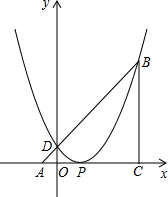
 与x轴交于点A(1,0)和点B,顶点为P.
与x轴交于点A(1,0)和点B,顶点为P.
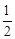 x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,―4).
x2+bx+c与y轴交于点C,与x轴相交于A,B两点,点A的坐标为(2,0),点C的坐标为(0,―4).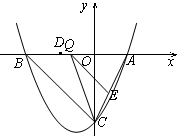
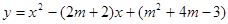 中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.
中,m为不小于0的整数,它的图像与x轴交于点A和点B,点A在原点左边,点B在原点右边.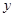 轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;
轴的交点,已知AD=AC(D在线段AB上),有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度移动,同时,另一动点Q从点C出发,以某一速度沿线段CB移动,经过t秒的移动,线段PQ被CD垂直平分,求t的值;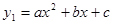 (
(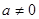 )与一次函数
)与一次函数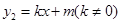 的图象相交于点A(-2,4),B(8,2)(如图所示),则能使y1<y2成立的
的图象相交于点A(-2,4),B(8,2)(如图所示),则能使y1<y2成立的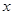 的取值范围是 .
的取值范围是 .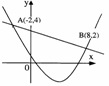
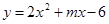 与x轴相交时两交点间的线段长为4,则m的值是 。
与x轴相交时两交点间的线段长为4,则m的值是 。