题目内容
有一种产品的质量分成6种不同档次,若工时不变,每天可生产最低档次的产品40件;如果每提高一个档次,每件利润可增加1元,但每天要少生产2件产品。
⑴若最低档次的产品每件利润17元时,生产哪一种档次的产品的利润最大?并求最大利润。
⑵由于市场价格浮动,生产最低档次的产品每件利润可以从8元到24元不等,那么生产哪种档次的产品所得利润最大?
⑴若最低档次的产品每件利润17元时,生产哪一种档次的产品的利润最大?并求最大利润。
⑵由于市场价格浮动,生产最低档次的产品每件利润可以从8元到24元不等,那么生产哪种档次的产品所得利润最大?
解:⑴设生产第X档次的产品,获得利润为y元,则

∴当X=2.5时,y的最大值为684.5
∵x为正整数
∴x=2时,y=684,x=3时,y=684,
∴当生产第2档次或第3档次的产品时所获得利润最,最大利润为684元
⑵设生产最低档次的产品每件利润为a元,生产第x档次的产品,获得利润为y元,则


∴当X=2.5时,y的最大值为684.5
∵x为正整数
∴x=2时,y=684,x=3时,y=684,
∴当生产第2档次或第3档次的产品时所获得利润最,最大利润为684元
⑵设生产最低档次的产品每件利润为a元,生产第x档次的产品,获得利润为y元,则

(1)先确定生产第x档次的产品,再表示出利润y的函数关系式,利用配方法求出最大利润;
(2)设生产最低档次的产品每件利润为a元,再表示出利润y的函数关系式,由x与a的关系可得x的值,再根据函数最值即可求得结果。
(2)设生产最低档次的产品每件利润为a元,再表示出利润y的函数关系式,由x与a的关系可得x的值,再根据函数最值即可求得结果。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
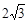 ,直线y=
,直线y=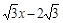 经过点C,交y轴于点G,且∠AGO=30°。
经过点C,交y轴于点G,且∠AGO=30°。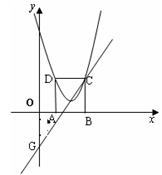
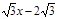 平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。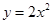 的图象向上平移1个单位,则平移后的抛物线的解析式为( )
的图象向上平移1个单位,则平移后的抛物线的解析式为( )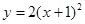
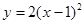
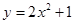
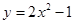
 的图象先向右平移4个单位,再向下平移3个单位所得的解析式为( )
的图象先向右平移4个单位,再向下平移3个单位所得的解析式为( )



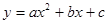 的图象,可知点(b,c)在第 象限.
的图象,可知点(b,c)在第 象限.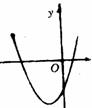

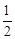 ;
;
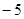 、
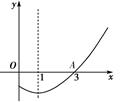
、 ,-1,0、1、3的6张卡片,背面完全相同,洗匀后,从中任取两张,该卡片上的数分别作为点P 的横坐标和纵坐标,P落在抛物线
,-1,0、1、3的6张卡片,背面完全相同,洗匀后,从中任取两张,该卡片上的数分别作为点P 的横坐标和纵坐标,P落在抛物线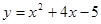 与对称轴右侧所围成的区域内(不含边界)的概率是 。
与对称轴右侧所围成的区域内(不含边界)的概率是 。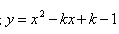 的顶点在坐标轴上,则k= .
的顶点在坐标轴上,则k= .