题目内容
【题目】若a、b是等腰△ABC的两边,且a是不等式组 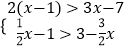 的最小整数解,b=46×0.256+(﹣
的最小整数解,b=46×0.256+(﹣ ![]() )﹣2﹣(3721﹣4568)0 , 求△ABC的周长.
)﹣2﹣(3721﹣4568)0 , 求△ABC的周长.
【答案】解: 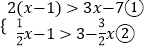
解不等式①,得x<5,
解不等式②,得x>2,
所以不等式组的解集是2<x<5,
因此,不等式组的最小整数解是3,即a=3,
∵b=46×0.256+(﹣ ![]() )﹣2﹣(3721﹣4568)0,
)﹣2﹣(3721﹣4568)0,
=(4×0.25)6+(﹣2)2﹣1=4,
当a=3为等腰三角形的底时,另外两腰都是b=4,
因为3+4=7,7大于4,能够成三角形
所以△ABC的周长是3+4+4=11,
当b=4为等腰三角形的底时,另外两腰都是a=3,
因为3+3=6,6大于4,能够成三角形
所以△ABC的周长是4+3+3=10,
所以△ABC的周长是10或11.
【解析】根据一次不等式组的解求得不等式组的整数解,再根据指数幂和等腰三角形的性质即可求出结论.
【考点精析】关于本题考查的零指数幂法则和一元一次不等式组的整数解,需要了解零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解)才能得出正确答案.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目