题目内容
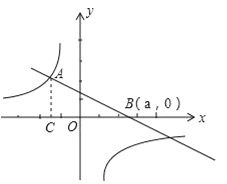
【题目】已知双曲线
和直线AB的图象交于点A（﹣3，4），AC⊥x轴于点C．
（1）求双曲线的解析式；
（2）当直线AB绕着点A转动时，与x轴的交点为B（a，0），并与双曲线另一支还有一个交点的情形下，求△ABC的面积S与a之间的函数关系式，并指出a的取值范围．
【答案】（1）
；（2）S=2a+6（a＞﹣3）．
【解析】
试题分析：（1）将点A（﹣3，4）代入反比例函数的解析式
，运用待定系数法即可求出双曲线的解析式；
（2）根据三角形的面积公式可求出△ABC的面积S与a之间的函数关系式，并根据直线AB与双曲线另一支还有一个交点即可求出a的取值范围．
试题解析：（1）将点A（﹣3，4）代入反比例函数的解析式，得4=
，解得k=﹣12，所以双曲线的解析式为；
（2）∵AC⊥x轴于点C，A（﹣3，4），∴C（﹣3，0），AC=4，∴BC=a﹣（﹣3）=a+3，∴S=
BCAC=（a+3）×4═2a+6，即S=2a+6．
∵当直线AB绕着点A转动时，与x轴的交点为B（a，0），并与双曲线另一支还有一个交点，∴a＞﹣3．
练习册系列答案
相关题目
