题目内容
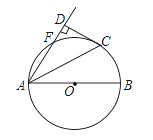
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE,BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD= ![]() AE2;④S△ABC=2S△ADF . 其中正确结论的序号是________.(把你认为正确结论的序号都填上)
AE2;④S△ABC=2S△ADF . 其中正确结论的序号是________.(把你认为正确结论的序号都填上)

【答案】①②③
【解析】
由直角三角形斜边上的中线性质得出FD=![]() AB,证明△ABE是等腰直角三角形,得出AE=BE,证出FE=
AB,证明△ABE是等腰直角三角形,得出AE=BE,证出FE=![]() AB,可得FD=FE,①正确;
AB,可得FD=FE,①正确;
证出∠ABC=∠C,得出AB=AC,由等腰三角形的性质得出BC=2CD,∠BAD=∠CAD=∠CBE,由ASA证明△AEH≌△BEC,得出AH=BC=2CD,②正确;
证明△ABD~△BCE,得出![]() =
=![]() ,即BCAD=ABBE,再由等腰直角三角形的性质和三角形的面积得出BCAD=
,即BCAD=ABBE,再由等腰直角三角形的性质和三角形的面积得出BCAD=![]() AE2;③正确;
AE2;③正确;
由F是AB的中点,BD=CD,得出S△ABC=2S△ABD=4S△ADF.④不正确;即可得出结论.
∵在△ABC中,AD和BE是高,
∴∠ADB=∠AEB=∠CEB=90°,
∵点F是AB的中点,
∴FD=![]() AB,
AB,
∵∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AE=BE,
∵点F是AB的中点,
∴FE=![]() AB,
AB,
∴FD=FE,①正确;
∵∠CBE=∠BAD,∠CBE+∠C=90°,∠BAD+∠ABC=90°,
∴∠ABC=∠C,
∴AB=AC,
∵AD⊥BC,
∴BC=2CD,∠BAD=∠CAD=∠CBE,
在△AEH和△BEC中,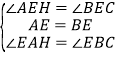 ,
,
∴△AEH≌△BEC(ASA),
∴AH=BC=2CD,②正确;
∵∠BAD=∠CBE,∠ADB=∠CEB,
∴△ABD△BCE,
∴![]() =
=![]() ,即BCAD=ABBE,
,即BCAD=ABBE,
∵△ABE是等腰直角三角形,
∴AB=![]() AE,
AE,
∵ABAE=ABBE =![]() ,BCAD=ACBE=ABBE,
,BCAD=ACBE=ABBE,
∴BCAD=![]() ;③正确;
;③正确;
∵F是AB的中点,BD=CD,
∴S△ABC=2S△ABD=4S△ADF.④不正确.
故答案为:①②③.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案