题目内容
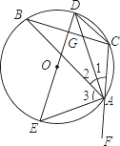
【题目】如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.
(1)求证:DE是△ABC的外接圆的直径;
(2)设OG=3,CD=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析 (2)5
【解析】
试题(1)根据条件AD、AE分别平分∠BAC和△BAC的外角∠BAF,证明∠2+∠3=90°即可;
(2)由∠1=∠2得出点D为弧BC的中点,从而得出DE垂直平分BC,连接BE,设圆的半径为r,然后证明△CDG∽△EBG,利用相似三角形的性质和勾股定理可求出r的值.
试题解析:(1)因为AD、AE分别是∠BAC和∠BAF的平分线
所以∠1=∠2=![]() ∠BAC, ∠3=∠EAF=
∠BAC, ∠3=∠EAF=![]() ∠BAF,
∠BAF,
所以∠2+∠3=![]() (∠BAC+∠BAF),
(∠BAC+∠BAF),
因为∠BAC+∠BAF=180°,
所以∠2+∠3=90°,
所以∠EAD=90°,
所以DE是圆O的直径;
(2)因为∠1=∠2,所以![]() ,又DE是△ABC的外接圆的直径,所以DE垂直平分BC,连接BE,则∠BEG=∠DCG,又∠BGE=∠DGC,所以△CDG∽△EBG,所以
,又DE是△ABC的外接圆的直径,所以DE垂直平分BC,连接BE,则∠BEG=∠DCG,又∠BGE=∠DGC,所以△CDG∽△EBG,所以![]() ,设圆的半径为r,所以
,设圆的半径为r,所以![]() ,又BG=CG,所以
,又BG=CG,所以![]() ,在Rt△CDG中,由勾股定理可得:
,在Rt△CDG中,由勾股定理可得:![]() ,解得r=5或r=-2(舍去),所以r=5.
,解得r=5或r=-2(舍去),所以r=5.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总数排列名次,在规定时间内每人踢100个以上(含100个)为优秀,下表是成绩最好的甲、乙两班各5名学生的比赛数据.(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
乙班 | 100 | 96 | 110 | 90 | 104 | 500 |
统计发现两班总数相等,此时有人建议,可以通过考查数据中的其他信息来评判.试从两班比赛数据的中位数、方差、优秀率三个方面考虑,你认为应该选定哪一个班为冠军?