Question

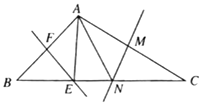
【题目】已知AB，BC，CD分别与⊙O相切于E，F，G三点，且AB∥CD，连接OB，OC．

（1）如图1，求∠BOC的度数；

（2）如图2，延长CO交⊙O于点M，过点M作MN∥OB交CD于点N，当OB=6，OC=8时，求⊙O的半径及MN的长．

Answer 1

【答案】（1）∠BOC=90°；（2）r=4.8；MN=9.6

【解析】

试题（1）根据平行得出∠ABC+∠DCB=180°，根据切线的性质可得，，得出∠OBC+∠OCB=90°，根据三角形内角和求出∠BOC的度数；（2）连接OF，根据切线得出∠OF⊥BC，根据（1）得出∠BOC=90°，根据勾股定理求出BC的长度，根据面积相等的法则求出OF的长度；根据△MCN和△OCB相似求出MN的长度.

试题解析（1）∵AB∥CD， ∴∠ABC+∠DCB=180°∵，，分别与⊙相切于，，三点，

∴，． ∴90°．

∴180°－=180°－90°=90°．

（2）连接，∵切⊙于点， ∴． 由（1）知，90°，

∴．∵，∴∴．

由（1）知，=90°，∴=90°．∵∥，∴=90°∴．

∵，分别切⊙于点，，∴．∴△∽△．

∴． 即． ∴．