Question

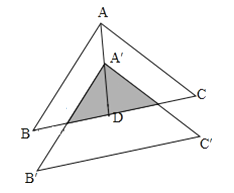
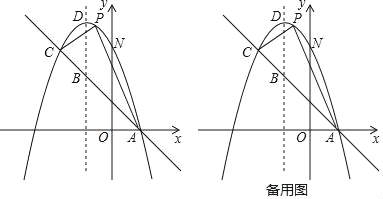
【题目】如图，已知△ABC中，AC＝BC，∠ACB＝120°，P为△ABC内部一点，且满足∠APB＝∠BPC＝150°．

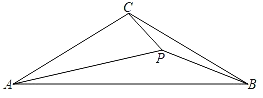
（1）求证：△PAB∽△PBC；

（2）求证：PA＝3PC；

（3）若AB＝10，求PA的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）PA＝

【解析】

（1）根据两角对应相等的两个三角形相似证明即可．

（2）过点C作CD⊥AB于D．首先证明，由△PAB∽△PBC，推出，可得结论．

（3）将线段BP绕点B顺时针旋转60°得到BP′，连接PP′，CP′，则△BPP′为等边三角形，在Rt△BCP′中，，，由（2）中，AB＝10，可得BC＝，利用勾股定理构建方程，求出PC即可解决问题．

（1）证明：∵△ABC中，AC＝BC，∠ACB＝120°，

∴∠CAB＝∠CBA＝（180°﹣120°）＝30°，

∴∠1+∠2＝30°，

∵∠APB＝150°，

∴∠2+∠3＝30°，

∴∠3＝∠1，

∵∠APB＝∠CPB，

∴△PAB∽△PBC．

（2）证明：过点C作CD⊥AB于D．

∵△ABC中，AC＝BC，

∴BD＝AB，

在Rt△CDB中，∠CBD＝30°，

∴，

∴，

∴，

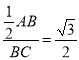∵△PAB∽△PBC，

∴，

∴PA＝PB，PB＝PC，

∴PA＝PC＝3PC．

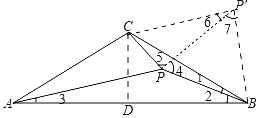
（3）解：将线段BP绕点B顺时针旋转60°得到BP′，连接PP′，CP′，则△BPP′为等边三角形，

∴∠4＝∠7＝60°，PP′＝PB＝BP′＝PC，

∴∠5＝∠BPC﹣∠4＝150°﹣60°＝90°，

在Rt△PP′C中，∠5＝90°，PP′＝PC，

∴tan∠6＝，

∴∠6＝60°，

∴∠6+∠7＝30°+60°＝90°，

∴P′C＝2PC，

∴在Rt△BCP′中，，，

由（2）中，AB＝10，可得BC＝，

∴（2PC）2+（PC）2＝（）2，

∴PC＝，

∴PA＝．