题目内容
【题目】如图,△ABC中,AB=AC,AD=BD=BC,则∠A的度数是( )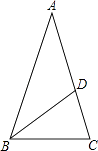
A.30°
B.36°
C.45°
D.20°
【答案】B
【解析】解:设∠A=x°.
∵BD=AD,
∴∠A=∠ABD=x°,(等边对等角)
∠BDC=∠A+∠ABD=2x°,(三角形的外角等于相邻两内角的和)
∵BD=BC,
∴∠BDC=∠BCD=2x°,(等边对等角)
∵AB=AC,
∴∠ABC=∠BCD=2x°,(等边对等角)
在△ABC中x+2x+2x=180,(三角形的内角和等于180°)
解得:x=36,
∴∠A=36°.
故答案为:B.
等腰三角形的性质1:等腰三角形的两个底角相等(简写“等边对等角”)
图中有多个与∠A有直接和间接关系的角,设其中∠A为未知量,代数思维解决几何问题。

练习册系列答案
相关题目