题目内容
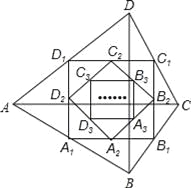
【题目】如图,四边形ABCD中,对角线AC⊥BD,且AC=8,BD=4,各边中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不确定
D. 不确定
【答案】B
【解析】试题分析:根据三角形的面积公式,可以求得四边形ABCD的面积是16;根据三角形的中位线定理,得A1B1∥AC,A1B1=A![]() C,则△BA1B1∽△BAC,得△BA1B1和△BAC的面积比是相似比的平方,即
C,则△BA1B1∽△BAC,得△BA1B1和△BAC的面积比是相似比的平方,即![]() ,因此四边形A1B1C1D1的面积是四边形ABCD的面积的
,因此四边形A1B1C1D1的面积是四边形ABCD的面积的![]() ,依此类推可得四边形AnBnCnDn的面积.
,依此类推可得四边形AnBnCnDn的面积.
∵四边形A1B1C1D1的四个顶点A1、B1、C1、D1分别为AB、BC、CD、DA的中点,
∴A1B1∥AC,A1B1=![]() AC, ∴△BA1B1∽△BAC, ∴△BA1B1和△BAC的面积比是相似比的平方,即
AC, ∴△BA1B1∽△BAC, ∴△BA1B1和△BAC的面积比是相似比的平方,即![]() ,
,
又四边形ABCD的对角线AC=8,BD=4,AC⊥BD, ∴四边形ABCD的面积是16,
∴SA1B1C1D1=![]() ×16, ∴四边形AnBnCnDn的面积=16×
×16, ∴四边形AnBnCnDn的面积=16×![]() =
=![]() .
.

练习册系列答案
相关题目