题目内容
【题目】已知△ABC是等腰直角三角形，∠BAC=90°，CD= 
BC，DE⊥CE，DE=CE，连接AE，点M是AE的中点．
（1）如图1，若点D在BC边上，连接CM，当AB=4时，求CM的长；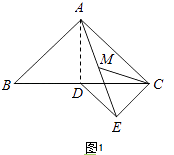 
（2）如图2，若点D在△ABC的内部，连接BD，点N是BD中点，连接MN，NE，求证：MN⊥AE； 
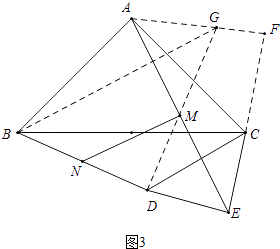
（3）如图3，将图2中的△CDE绕点C逆时针旋转，使∠BCD=30°，连接BD，点N是BD中点，连接MN，探索 
的值并直接写出结果． 
【答案】
（1）解：如图1中，连接AD．
∵△ABC是等腰直角三角形，
∴AB=AC=4，∠BAC=90°，
∴∠B=∠ACD=45°，BC= 
=4 
，
∵DC= 
BC=2 ，
∵ED=EC，∠DEC=90°，
∴DE=EC=2，∠DCE=∠EDC=45°，
∴∠ACE=90°，
在RT△ACE中，AE= 
= 
=2 
，
∵AM=ME，
∴CM= AE=
（2）解：如图2中，延长EN至F使NF=NE，连接AF、BF．
在△DNE和△BNF中，
，
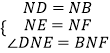∴△DNE≌△BNF，
∴BF=DE=EC，∠FBN=∠EDN，
∵∠ACB=∠DCE=45°，
∴∠ACE=90°﹣∠DCB，
∴∠ABF=∠FBN﹣∠ABN
=∠BDE﹣∠ABN
=180°﹣∠DBC﹣∠DGB﹣∠ABN
=180°﹣∠DBC﹣∠DCB﹣∠CDE﹣∠ABN
=180°﹣（∠DBC+∠ABN）﹣∠DCB﹣45°
=180°﹣45°﹣45°﹣∠DCB=90°﹣∠DCB=∠ACE，
在△ABF和△ACE中，
，
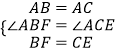∴△ABF≌△ACE．
∴∠FAB=∠EAC，
∴∠FAE=∠FAB+∠BAE=∠BAE+∠EAC=90°，
∵N为FE中点，M为AE中点，
∴AF∥NM，
∴MN⊥AE
（3）解：如图3中，延长DM到G使得MG=MD，连接AG、BG，延长AG、EC交于点F．
∵△AMG≌△EMD，
∴AG=DE=EC，∠GAM=∠DEM，
∴AG∥DE，
∴∠F=∠DEC=90°，
∵∠FAC+∠ACF=90°，∠BCD+∠ACF=90°，∠BCD=30°，
∴∠CAF=30°，∠BAG=∠BAC+∠CAF=120°，
∴∠BAG=∠ACE=120°，
在△ABG和△CAE中，
，
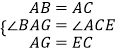∴△ABG≌△CAE，
∴BG=AE，
∵BN=ND，DM=MG，
∴BG=AE=2MN，
∵∠FAC=∠BCD=30°，设BC=2a，则CD=a，DE=EC= 
a，AC= a，CF= a，AF= 
a，EF= a，
∴AE= 
= 
a，
∴MN= 
a，
∴ 
= 
= 
．
【解析】（1）先证明△ACE是直角三角形，根据CM= AE，求出AE即可解决问题．（2）如图2中，如图2中，延长EN至F使NF=NE，连接AF、BF，先证明△DNE≌△BNF，再证明△ABF≌△ACE，推出∠FAB=∠EAC，可得∠FAE=∠FAB+∠BAE=∠BAE+∠EAC=90°，由此即可解决问题．（3）如图3中，延长DM到G使得MG=MD，连接AG、BG，延长AG、EC交于点F，先证明△ABG≌△CAE，得到BG=AE，设BC=2a，在RT△AEF中求出AE，根据中位线定理MN= BG= AE，由此即可解决问题．
【考点精析】根据题目的已知条件，利用勾股定理的概念的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
