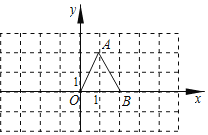题目内容
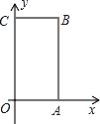
【题目】如图所示,在长方体![]() 中,
中,![]() 为平面直角坐标系的原点,
为平面直角坐标系的原点,![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,点
,点![]() 在第一象限.
在第一象限.
(1) 写出![]() 点坐标;
点坐标;
(2) 若过点![]() 的直线
的直线![]() ,且把
,且把![]() 分为
分为![]() :
:![]() 两部分,求出点
两部分,求出点![]() 的坐标;
的坐标;
(3) 在(2)的条件下,求出四边形![]() 的面积;
的面积;
(4) 若点![]() 是射线
是射线![]() 上的点,请直接写出
上的点,请直接写出![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1) 点B的坐标为(3,5);(2) 点D的坐标为(3,4)或(3,1);(3) ![]() 或9;(4) ∠APB=∠CBP+∠OAP或∠APB=∠CBP-∠OAP.
或9;(4) ∠APB=∠CBP+∠OAP或∠APB=∠CBP-∠OAP.
【解析】
(1)根据矩形的性质求出点B的横坐标与纵坐标即可得解;
(2)分AD是4份和1份两种情况讨论求出AD的长,从而得到点D的坐标;
(3)根据梯形的面积公式列式计算即可得解.
(4)分点P在原点上方和在原点下方两种情况求解:连接PB,PA,过点P作PE∥OA,根据平行线的性质可求得结论.
(1)∵A,C两点的坐标分别为(3,0),(0,5),
∴点B的横坐标为3,纵坐标为5,
∴点B的坐标为(3,5);
(2)如图,
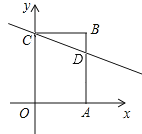
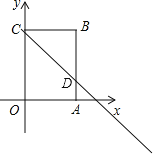
若AD为4份,则AD=5×![]() =4,
=4,
此时点D的坐标为(3,4),
若AD为1份,则AD=5×![]() =1,
=1,
此时点D的坐标为(3,1),
综上所述,点D的坐标为(3,4)或(3,1);
(3)AD=4时,四边形OADC的面积=![]() (4+5)×3=
(4+5)×3=![]() ,
,
AD=1时,四边形OADC的面积=![]() (1+5)×3=9,
(1+5)×3=9,
综上所述,四边形OADC的面积为![]() 或9.
或9.
(4)①当点P在原点上方时,连接PB,PA,过点P作PE∥OA,交AB于点E,如图,
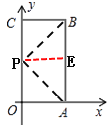
∵四边形OABC是矩形,
∴PE∥BC,
∴∠CBP=∠BPE,∠OAP=∠APE,
∵∠BPE+∠APE=∠CBP+∠OAP,即∠APB=∠CBP+∠OAP.
②当点P在原点下方时,连接PB,PA,过点P作PE∥OA,如图,
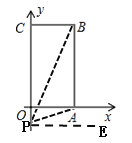
∵四边形OABC是矩形,
∴PE∥BC,
∴∠CBP=∠BPE,∠OAP=∠APE,
∵∠APB=∠BPE-∠APE,
∴∠APB=∠CBP-∠OAP.

 阅读快车系列答案
阅读快车系列答案