题目内容
【题目】如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依次类推,图10中有10个直角三角形的内切圆,它们的面积分别记为![]() ,
,![]() ,
,![]() ,…,
,…, ![]() ,则
,则![]() = .
= .

【答案】π
【解析】(1)如下图1,∵在△ABC中,∠C=90°,AC=3,BC=4,
∴由勾股定理可得:AB=![]() .
.
设△ABC的内切圆O的半径为![]() ,则
,则![]() ,
,
∴S⊙O= ![]() .
.
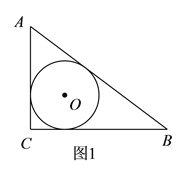
(2)如下图2,过点C作CD⊥AB于点D,则由S△ABC=![]() AC·BC=
AC·BC=![]() AB·CD可得:
AB·CD可得: ![]() CD,解得:CD=
CD,解得:CD=![]() ,
,
∴在Rt△ACD和Rt△BCD中,由勾股定理可解得:AD=![]() ,BD=
,BD=![]() ,
,
设⊙O1的半径为![]() ,⊙O2的半径为
,⊙O2的半径为![]() ,则
,则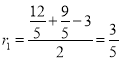 ,
, 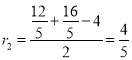 ,
,
∴S⊙O1+S⊙O2= ![]() .
.
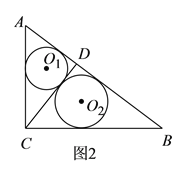
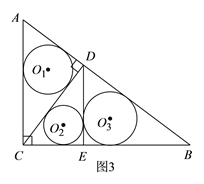
(3)如图3,过点D作DE⊥BC于点E,设三个圆的半径分别为![]() ,则同(2)可知
,则同(2)可知![]() ,可解得DE=
,可解得DE=![]() ,CE=
,CE=![]() ,BE=
,BE=![]() ,由此解得
,由此解得![]() ,
, ![]() ,
,
∴S⊙O1+S⊙O2+ S⊙O3= ![]() .
.
(4)综上所述,在图4中,S1+S2+S3+S4= ![]() ;
;
在图10中,S1+S2+S3+![]() +S10=
+S10= ![]() .
.

练习册系列答案
相关题目
【题目】小明家2015年的四个季度的用电量情况如表1,其中各种电器用电量情况如表2.
表1 | 表2 | |||
季度名称 | 用电量/度 | 电器 | 用电量/度 | |
第一季度 | 250 | 空调 | 250 | |
第二季度 | 150 | 冰箱 | 400 | |
第三季度 | 400 | 彩电 | 150 | |
第四季度 | 200 | 其他 | 100 | |
小明根据上面的数据制成如图所示的统计图.


根据以上三幅统计图回答下列问题:
(1)从哪幅统计图中可以看出各季度用电量变化情况?
(2)从哪幅统计图中可以看出冰箱的用电量超过总用电量的![]() ?
?
(3)从哪幅统计图中可以清楚地看出空调的用电量?