题目内容
【题目】已知∠MON=![]() ,P为射线OM上的点,OP=1.
,P为射线OM上的点,OP=1.
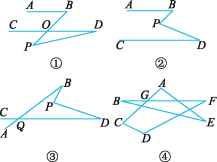
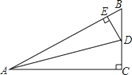
(1)如图1,![]() ,A,B均为射线ON上的点,OA=1,OB
,A,B均为射线ON上的点,OA=1,OB![]() OA,△PBC为等边三角形,且O,C两点位于直线PB的异侧,连接AC.
OA,△PBC为等边三角形,且O,C两点位于直线PB的异侧,连接AC.
①依题意将图1补全;
②判断直线AC与OM的位置关系并加以证明;
(2)若![]() ,Q为射线ON上一动点(Q与O不重合),以PQ为斜边作等腰直角△PQR,使O,R两点位于直线PQ的异侧,连接OR. 根据(1)的解答经验,直接写出△POR的面积.
,Q为射线ON上一动点(Q与O不重合),以PQ为斜边作等腰直角△PQR,使O,R两点位于直线PQ的异侧,连接OR. 根据(1)的解答经验,直接写出△POR的面积.
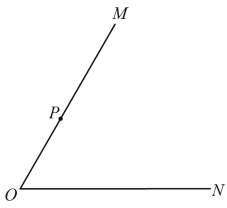
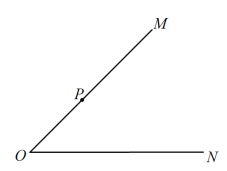
图1 备用图
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)①依据题意画图即可;
②连接AP,通过证明△OBP≌△ACP得![]() ,从而
,从而![]() ,根据平行线的性质得
,根据平行线的性质得![]() .
.
(2)根据勾股定理得到△POR的OP边的长,根据三角形的面积公式即可得到结论.
解:(1)①依题意,将图1补全;
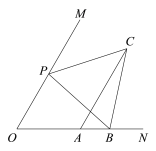
②![]() .
.
证明:连接AP,
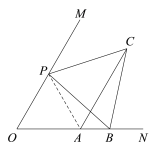
∵![]() ,
,![]() ,
,
∴△OAP是等边三角形.
∴![]() .
.
∵△PBC是等边三角形,
∴![]() .
.
∴![]() .
.
即![]() .
.
∴△OBP≌△ACP.
∴![]() .
.
∴![]() .
.
∴![]() .
.
(2)![]() .
.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目