题目内容
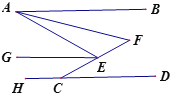
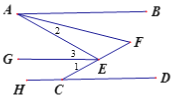
【题目】如图,已知AB∥HD,EG平分∠AEC,EG∥AB,AF平分∠BAE,CE的延长线交AF于点F,若∠HCE=![]() °,∠F=
°,∠F=![]() °,用含
°,用含![]() 的代数式表示
的代数式表示![]() ,则
,则![]() =_______
=_______
【答案】270-![]() x
x
【解析】
由角平分线定义可得∠AEC=2∠1,∠1=∠3,∠2=![]() ∠EAB,由AB∥HD, EG∥AB,可得∠BAE=∠3,EG//HD,继而可得∠1、∠AEC、∠2,再由三角形外角的性质可知∠2+∠F=∠AEC,代入相关式子即可求得答案.
∠EAB,由AB∥HD, EG∥AB,可得∠BAE=∠3,EG//HD,继而可得∠1、∠AEC、∠2,再由三角形外角的性质可知∠2+∠F=∠AEC,代入相关式子即可求得答案.
∵EG平分∠AEC, AF平分∠BAE,
∴∠AEC=2∠1,∠1=∠3,∠2=![]() ∠EAB,
∠EAB,
∵AB∥HD, EG∥AB,
∴∠BAE=∠3,EG//HD,
∴∠1=180°-∠HCE=180°-x°,
∴∠AEC=2(180°-x°),∠2=![]() (180°-x°),
(180°-x°),
∵∠2+∠F=∠AEC,
∴![]() (180°-x°)+y°=2(180°-x°),
(180°-x°)+y°=2(180°-x°),
∴y=270-![]() x,
x,
故答案为:270-![]() x.
x.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
【题目】一蓄水池有水40m3,按一定的速度放水,水池里的水量y (m3)与放水时间t(分)有如下关系:
放水时间(分) | 1 | 2 | 3 | 4 | ... |
水池中水量(m) | 38 | 36 | 34 | 32 | ... |
下列结论中正确的是
A. y随t的增加而增大B. 放水时间为15分钟时,水池中水量为8m3
C. 每分钟的放水量是2m3D. y与t之间的关系式为y=38-2t





