题目内容
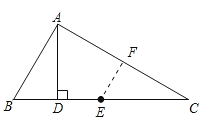
【题目】如图，Rt△ACB中，∠ACB=90°，∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P，分别交AC和BC的延长线于E，D．过P作PF⊥AD交AC的延长线于点H，交BC的延长线于点F，连接AF交DH于点G．则下列结论：①∠APB=45°；②PF=PA；③BD﹣AH=AB；④DG=AP+GH．其中正确的是（ ）
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
①根据三角形的一个外角等于与它不相邻的两个内角的和与角平分线的定义表示出∠CAP，再根据角平分线的定义∠ABP=
∠ABC，然后利用三角形的内角和定理整理即可得解；
②先求出∠APB=∠FPB，再利用“角边角”证明△ABP和△FBP全等，根据全等三角形对应边相等得到AB=BF，AP=PF；
③根据直角的关系求出∠AHP=∠FDP，然后利用“角角边”证明△AHP与△FDP全等，根据全等三角形对应边相等可得DF=AH；
④根据PF⊥AD，∠ACB=90°，可得AG⊥DH，然后求出∠ADG=∠DAG=45°，再根据等角对等边可得DG=AG，再根据等腰直角三角形两腰相等可得GH=GF，然后求出DG=GH+AF，有直角三角形斜边大于直角边，AF＞AP，从而得出本小题错误.
解：①∵∠ABC的角平分线BE和∠BAC的外角平分线，
∴∠ABP=∠ABC，
∠CAP=（90°+∠ABC）=45°+∠ABC，
在△ABP中，∠APB=180°-∠BAP-∠ABP，
=180°-（45°+∠ABC+90°-∠ABC）-∠ABC，
=180°-45°- ∠ABC-90°+∠ABC-∠ABC，
=45°，故本小题正确；
②∵PF⊥AD，∠APB=45°（已证），
∴∠APB=∠FPB=45°，
∵∵PB为∠ABC的角平分线，
∴∠ABP=∠FBP，
在△ABP和△FBP中，
，
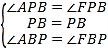∴△ABP≌△FBP（ASA），
∴AB=BF，AP=PF；故②正确；
③∵∠ACB=90°，PF⊥AD，
∴∠FDP+∠HAP=90°，∠AHP+∠HAP=90°，
∴∠AHP=∠FDP，
∵PF⊥AD，
∴∠APH=∠FPD=90°，
在△AHP与△FDP中，
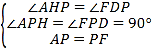
∴△AHP≌△FDP（AAS），
∴DF=AH，
∵BD=DF+BF，
∴BD=AH+AB，
∴BD-AH=AB，故③小题正确；
④∵PF⊥AD，∠ACB=90°，
∴AG⊥DH，
∵AP=PF，PF⊥AD，
∴∠PAF=45°，
∴∠ADG=∠DAG=45°，
∴DG=AG，
∵∠PAF=45°，AG⊥DH，
∴△ADG与△FGH都是等腰直角三角形，
∴DG=AG，GH=GF，
∴DG=GH+AF，
∵AF＞AP，
∴DG=AP+GH不成立，故本小题错误，
综上所述①②③正确．
故选:C.
