题目内容
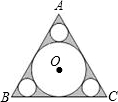如图，已知正三角形ABC的边长为6，在△ABC中作内切圆O及三个角切圆（我们把与角两边及三角形内切圆都相切的圆叫角切圆），则△ABC的内切圆O的面积为分析：连接OB，以及⊙O与BC的切点，在构造的直角三角形中，通过解直角三角形易求得⊙O的半径为
；然后作⊙O与小圆的公切线EF，易知△BEF也是等边三角形，那么小圆的圆心也是等边△BEF的重心；由此可求得小圆的半径，即可得到四个圆的面积，从而由等边三角形的面积减去四个圆的面积和即为阴影部分的面积．
| 3 |
解答：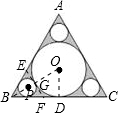
解：如图，连接OB、OD；设小圆的圆心为P，⊙P与⊙O的交点为G；
过G作两圆的公切线EF，交AB于E，交BC于F；
则∠BEF=∠BFE=90°-30°=60°，所以△BEF是等边三角形；
在Rt△OBD中，BD=3，∠OBD=30°，则OD=
，OB=2
，BG=
；
由于⊙P是等边△BEF的内切圆，所以点P是△BEF的内心，也是重心，
故PG=
BG=
；
∴S⊙O=π×（
）2=3π，S⊙P=π×（
）2=
π；
∴S阴影=S△ABC-S⊙O-3S⊙P=9
-3π-π=9
-4π；
故△ABC的内切圆O的面积为3π，图中阴影部分的面积为9
-4π．
解：如图，连接OB、OD；设小圆的圆心为P，⊙P与⊙O的交点为G；过G作两圆的公切线EF，交AB于E，交BC于F；
则∠BEF=∠BFE=90°-30°=60°，所以△BEF是等边三角形；
在Rt△OBD中，BD=3，∠OBD=30°，则OD=
| 3 |
| 3 |
| 3 |
由于⊙P是等边△BEF的内切圆，所以点P是△BEF的内心，也是重心，
故PG=
| 1 |
| 3 |
| ||
| 3 |
∴S⊙O=π×（
| 3 |
| ||
| 3 |
| 1 |
| 3 |
∴S阴影=S△ABC-S⊙O-3S⊙P=9
| 3 |
| 3 |
故△ABC的内切圆O的面积为3π，图中阴影部分的面积为9
| 3 |
点评：此题主要考查了等边三角形的性质、相切两圆的性质以及图形面积的计算方法，难度适中．
练习册系列答案
发散思维新课堂系列答案
相关题目
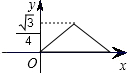
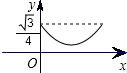
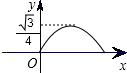
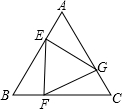如图，已知正三角形ABC的边长为1，E，F，G分别是AB，BC，CA上的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y关于x的函数的图象大致是（ ）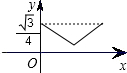
29、如图，已知正三角形的边长2a
点A运动．
