题目内容
归纳猜想:同学们,让我们一起进行一次研究性学习:
(1)如图1已知正三角形ABC的中心为O,半径为R,将其沿直线l向右翻滚,当正三角形翻滚一周时,其中心O经过的路程是多少?

(2)如图2将半径为R的正方形沿直线l向右翻滚,当正方形翻滚一周时,其中心O经过的路程是多少?

(3)猜想:把正多边形翻滚一周,其中心O所经过的路程是多少(R为正多边形的半径,可参看图2)?请说明理由.
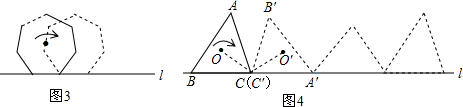
(4)进一步猜想:任何多边形都有一个外接圆,若将任意圆内接多边形翻滚一周时,其外心所经过的路程是否是一个定值(R为多边形外接圆的半径)?为什么?请以任意三角形为例说明(如图12).
通过以上猜想你可得到什么样的结论?请写出来.
(1)如图1已知正三角形ABC的中心为O,半径为R,将其沿直线l向右翻滚,当正三角形翻滚一周时,其中心O经过的路程是多少?

(2)如图2将半径为R的正方形沿直线l向右翻滚,当正方形翻滚一周时,其中心O经过的路程是多少?

(3)猜想:把正多边形翻滚一周,其中心O所经过的路程是多少(R为正多边形的半径,可参看图2)?请说明理由.

(4)进一步猜想:任何多边形都有一个外接圆,若将任意圆内接多边形翻滚一周时,其外心所经过的路程是否是一个定值(R为多边形外接圆的半径)?为什么?请以任意三角形为例说明(如图12).
通过以上猜想你可得到什么样的结论?请写出来.
分析:(1)当正三角形ABC向右翻滚一周时,其中心O经过的路线是三条等弧,根据弧长公式求出一条弧长,继而可得出答案.
(2)滚过的路程相当于90°的圆弧的长,继而代入弧长公式计算即可.
(3)当n边形向右翻滚一周时,其中心O经过的路线是n条等弧,这些弧的半径为R,所对的圆心角为
,继而代入计算即可.
(4)是定值2πR,按照前面的计算思想进行证明即可.
(2)滚过的路程相当于90°的圆弧的长,继而代入弧长公式计算即可.
(3)当n边形向右翻滚一周时,其中心O经过的路线是n条等弧,这些弧的半径为R,所对的圆心角为
| 360° |
| n |
(4)是定值2πR,按照前面的计算思想进行证明即可.
解答:解:(1)当正三角形ABC向右翻滚一周时,其中心O经过的路线是三条等弧,
所以其中心O经过的路程为:
×3=2πR.
(2)中心O经过的路程为
×4=2πR.
(3)当n边形向右翻滚一周时,其中心O经过的路线是n条等弧,这些弧的半径为R,所对的圆心角为
,
所以中心O经过的路程为
×n=2πR.
(4)是定值2πR,理由如下:
在△ABC中,设∠A=α,∠B=β,∠C=γ,△ABC的外接圆⊙O的半径为R,
把△ABC沿直线l向右翻滚一周时,其外心O经过的路线是三条弧,
当AC边与直线l重合时,C与C'重合,A与A'重合,B与B'重合,
连接CO、C'O',则∠ACO=∠A'C'O',
所以∠OCO'=∠ACA'=180°-γ,
所以l=
,
同理,另两条弧长分别为:
,
,
所以外心O所经过的路程为2πR.
通过以上猜想可得结论为:把圆内接多边形翻滚一周时,多边形的外心所经过的路程是一个定值.
所以其中心O经过的路程为:
| 120πR |
| 180 |
(2)中心O经过的路程为
| 90πR |
| 180 |
(3)当n边形向右翻滚一周时,其中心O经过的路线是n条等弧,这些弧的半径为R,所对的圆心角为
| 360° |
| n |
所以中心O经过的路程为
| ||
| 180 |
(4)是定值2πR,理由如下:
在△ABC中,设∠A=α,∠B=β,∠C=γ,△ABC的外接圆⊙O的半径为R,
把△ABC沿直线l向右翻滚一周时,其外心O经过的路线是三条弧,
当AC边与直线l重合时,C与C'重合,A与A'重合,B与B'重合,
连接CO、C'O',则∠ACO=∠A'C'O',
所以∠OCO'=∠ACA'=180°-γ,
所以l=
| (180-γ)πR |
| 180 |
同理,另两条弧长分别为:
| (180-α)πR |
| 180 |
| (180-β)πR |
| 180 |
所以外心O所经过的路程为2πR.
通过以上猜想可得结论为:把圆内接多边形翻滚一周时,多边形的外心所经过的路程是一个定值.
点评:此题考查了弧长的计算,解答本题的关键是掌握一些特殊图形的性质,熟练记忆弧长公式,有一定的难度,注意培养猜测、推理能力.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目





