题目内容
如图,已知正三角形ABC的边长AB是480毫米.一质点D从点B出发,沿BA方向,以每秒钟10毫米的速度向 点A运动.
点A运动.(1)建立合适的直角坐标系,用运动时间t(秒)表示点D的坐标;
(2)过点D在三角形ABC的内部作一个矩形DEFG,其中EF在BC边上,G在AC边上.在图中找出点D,使矩形DEFG是正方形(要求所表达的方式能体现出找点D的过程);
(3)过点D、B、C作平行四边形,当t为何值时,由点C、B、D、F组成的平行四边形的面积等于三角形ADC的面积,并求此时点F的坐标.
分析:运用相似三角形及平行四边形的性质求解.
解答:解:(1)建立如图所示的直角坐标系,作DE⊥x轴于E,
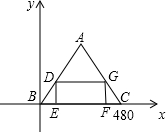
则t秒后,DB=10t
又△ABC是正三角形,故∠B=60°
在Rt△DEB中,DE=DB×sin∠B=10t×
=5
t,
BE=DB×cos∠B=10t×
=5t
即:D(5t,5
t);
(2)①先画一个正方形,再利用位似图形找出点D,具体作法阅图
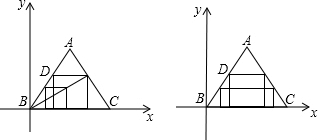
②利用正三角形与矩形是轴对称图形或利用相似三角形
的性质求得DG=480-10t,DE=5
t.然后由480-10t=5
t
求出t=
=96(2-
)(毫米).所以当点D与点B的距离
等于10t=960(2-
)毫米时,矩形是正方形.
(3)如图所示:
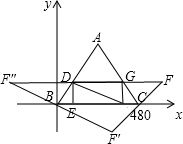
当点F在第一象限时,这个平行四边形是CBDF;
当点F在第二象限时,这个平行四边形是BCDF“;
当点F在第三象限时,这个平行四边形是CDBF'.
但平行四边形BCDF“的面积、平行四边形CDBF'的面积
都与平行四边形CBDF的面积相等(等底等高)
平行四边形CBDF的底BC=480,相应的高是5
t,则面积是2400
t;三角形ADC的底AD=480-10t,相应的高是240
则面积是120
(480-10t).
由2400
t=120
(480-10t),解得t=16
所以当t=16秒时,由点C、B、D、F组成的平
行四边形的面积等于三角形ADC的面积.
∴此时,点F的坐标是F(560,80
),F′(400,-80
)
F″(-400,80
).

则t秒后,DB=10t
又△ABC是正三角形,故∠B=60°
在Rt△DEB中,DE=DB×sin∠B=10t×
| ||
| 2 |
| 3 |
BE=DB×cos∠B=10t×
| 1 |
| 2 |
即:D(5t,5
| 3 |
(2)①先画一个正方形,再利用位似图形找出点D,具体作法阅图

②利用正三角形与矩形是轴对称图形或利用相似三角形
的性质求得DG=480-10t,DE=5
| 3 |
| 3 |
求出t=
| 96 | ||
2+
|
| 3 |
等于10t=960(2-
| 3 |
(3)如图所示:

当点F在第一象限时,这个平行四边形是CBDF;
当点F在第二象限时,这个平行四边形是BCDF“;
当点F在第三象限时,这个平行四边形是CDBF'.
但平行四边形BCDF“的面积、平行四边形CDBF'的面积
都与平行四边形CBDF的面积相等(等底等高)
平行四边形CBDF的底BC=480,相应的高是5
| 3 |
| 3 |
| 3 |
则面积是120
| 3 |
由2400
| 3 |
| 3 |
所以当t=16秒时,由点C、B、D、F组成的平
行四边形的面积等于三角形ADC的面积.
∴此时,点F的坐标是F(560,80
| 3 |
| 3 |
F″(-400,80
| 3 |
点评:本题考查对相似三角形的运用能力和平行四边形的性质掌握程度.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
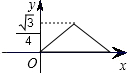
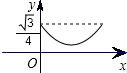
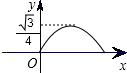
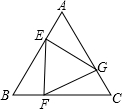 如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )
如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )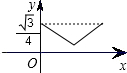
 29、如图,已知正三角形的边长2a
29、如图,已知正三角形的边长2a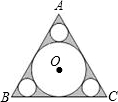 如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为
如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为