题目内容
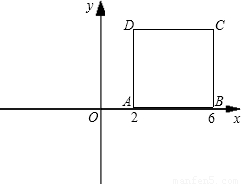
 如图,在坐标系中有一点A(-1,2),关于直线x=1对称得点B,将点B向上平移m个单位得到点C,
如图,在坐标系中有一点A(-1,2),关于直线x=1对称得点B,将点B向上平移m个单位得到点C,(1)用m表示C点的坐标;
(2)在x轴上存在一点P(n,0),使PA+PC的值最小,求n的值.
分析:(1)因为A和B关于直线x=1对称,所以可以求出B的坐标,又因为C是将点B向上平移m个单位得,根据平移的规律可得到C的坐标;
(2)作点A关于x轴的对称点A′,连接A′C,其与x轴的交点即为所求的点P.
(2)作点A关于x轴的对称点A′,连接A′C,其与x轴的交点即为所求的点P.
解答:解(1)∵点A(-1,2),点B和点A关于直线x=1对称,
∴B点的坐标为(3,2),
∵将点B向上平移m个单位得到点C,
∴C点D的坐标是(3,2+m);
(2)作点A关于x轴的对称点A′,连接A′C,A′C与x轴的交点即为所求的点P,
则点A关于x轴的对称点A′(-1,-2),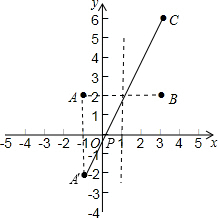
设直线CA′的解析式为y=kx+b,
过点C(3,2+m)和A′(-1,-2),
∴
,
解得:
,
∴y=(1+
)x-1+
,
∵y=(1+
)x-1+
与x轴的交点就是y=0时,
即(1+
)x-1+
=0,
解得:x=
,
∴点P的坐标是(
,0).
即存在这样的点P使PA+PC的值最小,P点的坐标为(
,0).
∴B点的坐标为(3,2),
∵将点B向上平移m个单位得到点C,
∴C点D的坐标是(3,2+m);
(2)作点A关于x轴的对称点A′,连接A′C,A′C与x轴的交点即为所求的点P,
则点A关于x轴的对称点A′(-1,-2),
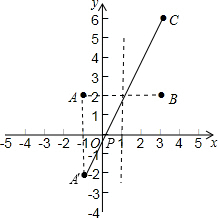
设直线CA′的解析式为y=kx+b,
过点C(3,2+m)和A′(-1,-2),
∴
|
解得:
|
∴y=(1+
| m |
| 4 |
| m |
| 4 |
∵y=(1+
| m |
| 4 |
| m |
| 4 |
即(1+
| m |
| 4 |
| m |
| 4 |
解得:x=
1-
| ||
1+
|
∴点P的坐标是(
1-
| ||
1+
|
即存在这样的点P使PA+PC的值最小,P点的坐标为(
1-
| ||
1+
|
点评:本题考查轴对称-最短路线问题,注意掌握两点关于某条直线对称,横纵坐标中有一个坐标是相等的,另一坐标为2×对称轴-已知点的坐标;凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合本节所学轴对称变换来解决,多数情况要作点关于某直线的对称点.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
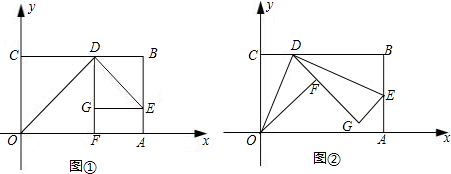
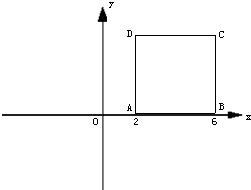 30、如图,直角坐标系中有一正方形ABCD,若以O为中心把正方形ABCD缩小为原来的一半,则得正方形A′B′C′D′.
30、如图,直角坐标系中有一正方形ABCD,若以O为中心把正方形ABCD缩小为原来的一半,则得正方形A′B′C′D′.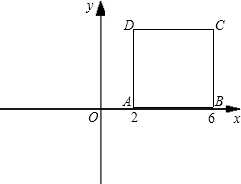 (1)在图中画出正方形A′B′C′D′.
(1)在图中画出正方形A′B′C′D′.