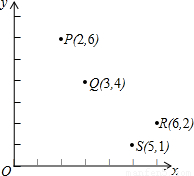题目内容
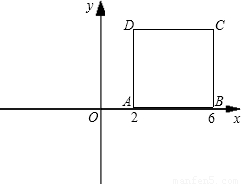
如图,直角坐标系中有一正方形ABCD,若以O为中心把正方形ABCD缩小为原来的一半,则得正方形A′B′C′D′.
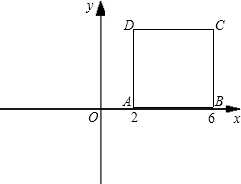 (1)在图中画出正方形A′B′C′D′.
(1)在图中画出正方形A′B′C′D′.
(2)写出A′、B′、C′、D′的坐标.
 解:(1)画图如图所示;
解:(1)画图如图所示;(2)∵A(2,0),B(6,0),
∴AB=BC=CD=DA=4,
∴C(6,4),D(2,4),
∵正方形ABCD,以O为位似中心,把正方形ABCD的面积缩小为原来的一半,得正方形A′B′C′D′,′
有两种情况:
①A′(1,0).B′(3,0)、C′(3,2)、D′(1,2),
②A″(-1,0)、B″(-3,0)、C″(-3,-2)、D″(-1,-2).
分析:首先由A与B的坐标,求得点C与D的坐标,又由正方形ABCD,以O为位似中心,把正方形ABCD缩小为原来的一半,得正方形A′B′C′D′,根据位似变换的性质即可求得A′B′、C′、D′的坐标.
点评:此题主要考查了位似变换的性质.注意数形结合思想的应用是解此题的关键,还要小心不要漏解.

练习册系列答案
相关题目
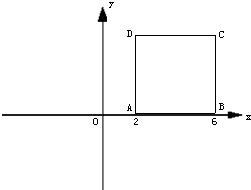 30、如图,直角坐标系中有一正方形ABCD,若以O为中心把正方形ABCD缩小为原来的一半,则得正方形A′B′C′D′.
30、如图,直角坐标系中有一正方形ABCD,若以O为中心把正方形ABCD缩小为原来的一半,则得正方形A′B′C′D′.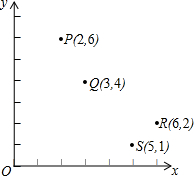 (2011•葫芦岛)如图,直角坐标系中有四个点,其中的三点在同一反比例函数的图象上,则不在这个图象上的点是( )
(2011•葫芦岛)如图,直角坐标系中有四个点,其中的三点在同一反比例函数的图象上,则不在这个图象上的点是( )