题目内容
如图,正方形ABCD的边长为2cm,在对称中心O处有一钉子.动点P,Q同时从点A出发,点P沿A?B?C方向以每秒2cm的速度运动,到点C停止,点Q沿A?D方向以每秒1cm的速度运动,到点D停止.P,Q两点用一条可伸缩的细橡皮筋连接,设x秒后橡皮筋扫过的面积为ycm2.
(1)当0≤x≤1时,求y与x之间的函数关系式;
(2)当橡皮筋刚好触及钉子时,求x值;
(3)当1≤x≤2时,求y与x之间的函数关系式,并写出橡皮筋从触及钉子到运动停止时∠POQ的变化范围;
(4)当0≤x≤2时,请在给出的直角坐标系中画出y与x之间的函数图象.
(1)当0≤x≤1时,求y与x之间的函数关系式;
(2)当橡皮筋刚好触及钉子时,求x值;
(3)当1≤x≤2时,求y与x之间的函数关系式,并写出橡皮筋从触及钉子到运动停止时∠POQ的变化范围;
(4)当0≤x≤2时,请在给出的直角坐标系中画出y与x之间的函数图象.

(1)当0≤x≤1时,AP=2x,AQ=x,y=
AQ•AP=x2,
即y=x2.
(2)当S四边形ABPQ=
S正方形ABCD时,橡皮筋刚好触及钉子,
BP=2x-2,AQ=x,
(2x-2+x)×2=
×22,∴x=
.
(3)当1≤x≤
时,AB=2,PB=2x-2,AQ=x,
∴y=
•AB=
×2=3x-2,
即y=3x-2.
作OE⊥AB,E为垂足.
当
≤x≤2时,
BP=2x-2,AQ=x,OE=1,y=S梯形BEOP+S梯形OEAQ=
×1+
×1=
x,
即y=
x.(6分)
90°≤∠POQ≤180°.
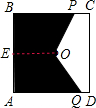
(4)如图所示:
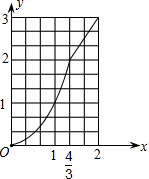 .
.
| 1 |
| 2 |
即y=x2.
(2)当S四边形ABPQ=
| 1 |
| 2 |
BP=2x-2,AQ=x,
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
(3)当1≤x≤
| 4 |
| 3 |
∴y=
| AQ+BP |
| 2 |
| x+2x-2 |
| 2 |
即y=3x-2.
作OE⊥AB,E为垂足.
当
| 4 |
| 3 |
BP=2x-2,AQ=x,OE=1,y=S梯形BEOP+S梯形OEAQ=
| 1+2x-2 |
| 2 |
| 1+x |
| 2 |
| 3 |
| 2 |
即y=
| 3 |
| 2 |
90°≤∠POQ≤180°.

(4)如图所示:
 .
.
练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目

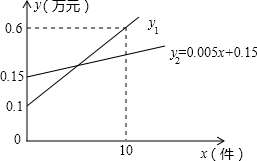
 BP交⊙P于点C
BP交⊙P于点C B点,同时点Q以2米/分的速度从点B移动到C点(当一个点到达后全部停止移动).
B点,同时点Q以2米/分的速度从点B移动到C点(当一个点到达后全部停止移动).


