题目内容
【题目】阅读并解决问题:归纳
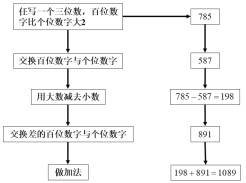
人们通过长期观察发现,如果早晨天空中有棉絮状的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学里,我们也常用这样的方法探求规律,例如:三角形有3个顶点,如果在它的内部再画n个点,并以(n+3)个点为顶点,把三角形剪成若干个小三角形,那么最多可以剪得多少个这样的三角形? .为了解决这个问题,我们可以从n=1、n=2、nr=3 等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.

(1)完成表格信息:_______、_________;
(2)通过观察、比较,可以发现:三角形内的点每增加1个,最多可以剪得的三角形增加_________个.于是,我们可以猜想:当三角形内的点的个数为n时,最多可以剪得____________个三角形.像这样通过对现象的观察、分析,从特殊到-般地探索这类现象的规律、提出猜想的思想方法称为归纳.在日常生活中,人们互相交谈时,常常有人在列举了一些现象后,说“这(即列举的现象)说明....其实这就是运用了归纳的方法.用归纳的方法得出的结论不一定正确,是否正确需要加以证实.
(3)请你借助表格尝试用归纳的方法探索: 1+3+5+7+......+(2n-1)的和是多少?并加以证实.
【答案】(1)5,7;(2)2,2n+1;(3)S=n2,见解析
【解析】
(1)由图形规律可得,答案为5,7;
(2)因为5-3=7-5=2,所以三角形内的点每增加1个,最多可以剪得的三角形增加2个;∵三角形内点的个数为1时,最多剪出的小三角形个数3=2×1+1,因为三角形内点的个数为2时,最多剪出的小三角形个数5=2×2+1,三角形内点的个数为3时,7最多剪出的小三角形个数7=2×3+1,所以三角形内点的个数为n时,最多剪出的小三角形个数2n+1;
(3)用倒序相加法证明即可.
(1)把表格补充完整如下:
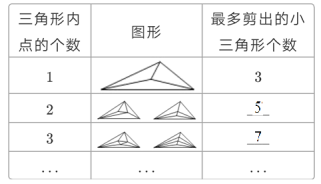
故答案为:5,7;
(2)∵5-3=7-5=2,
∴三角形内的点每增加1个,最多可以剪得的三角形增加2个;
∵三角形内点的个数为1时,最多剪出的小三角形个数3=2×1+1,
三角形内点的个数为2时,最多剪出的小三角形个数5=2×2+1,
三角形内点的个数为3时,7最多剪出的小三角形个数7=2×3+1,
……
∴三角形内点的个数为n时,最多剪出的小三角形个数为2n+1.
故答案为2,(2n+1);
(3)
证明:∵S=1+3+5+7+…+(2n-5)+(2n-3)+(2n-1),
∴S=(2n-1)+(2n-3)+(2n-5)+…+7+5+3+1,
∴S+S=2nn=2n2,
2S=2n2
S=n2

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】甲乙两位同学参加数学综合素质测试,各项成绩如下表:(单位:分)
数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
学生甲 | 93 | 93 | 89 | 90 |
学生乙 | 94 | 92 | 94 | 86 |
(1)分别计算甲、乙同学成绩的中位数;
(2)如果数与代数,空间与图形,统计与概率,综合与实践的成绩按4:3:1:2计算,那么甲、乙同学的数学综合素质成绩分别为多少分?
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛,成绩如图所示:
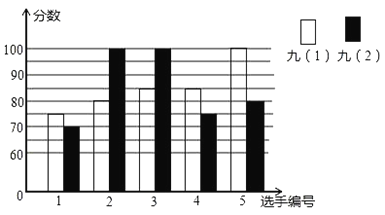
(1)根据图示填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | ||
九(2) | 85 | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)已知九(1)班复赛成绩的方差是70,请计算九(2)班的复赛成绩的方差,并说明哪个班的成绩比较稳定?