Question

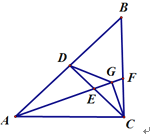
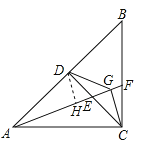
【题目】如图，在等腰直角三角形ABC中，AC=BC,AB=4,D是AB的中点，连结DC，E为DC中点，连接AE，延长AE交BC于F,过点C作CG⊥AF,垂足是G，连接DG,则∠DGA=_______，DG=________

Answer 1

【答案】 45° 2

【解析】根据等腰直角三角形的性质得到CD⊥AB，CD=AB=2，∠ACD=∠BCD=45°，再由CG⊥AF，所以∠ADC=∠AGC=90°，即可判定点A，C，G，D四点共圆，根据圆周角定理得到∠DGA=∠ACD=45°；过D作DH⊥AF于H，得到△DHG是等腰直角三角形，根据点E为CD的中点，求得DE=CD=，根据勾股定理得到AE==5，根据三角形的面积公式得到DH=，在等腰直角三角形△DHG即可求得DG=2.