题目内容
【题目】如图所示，我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度．小宇同学在A处观测对岸C点，测得∠CAD=45°，小英同学在距A处50米远的B处测得∠CBD=30°，请你根据这些数据算出河宽．（精确到0.01米，参考数据 
≈1.414， 
≈1.732） 
【答案】解：过C作CE⊥AB于E，设CE=x米， 在Rt△AEC中：∠CAE=45°，AE=CE=x
在Rt△BCE中：∠CBE=30°，BE= 
CE= x，
∴ x=x+50解之得：x=25 +25≈68.31．
答：河宽为68.31米．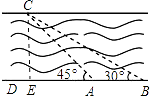
【解析】设河宽为未知数，那么可利用三角函数用河宽表示出AE、EB，然后根据BE﹣AE=50就能求得河宽．
优翼小帮手同步口算系列答案【题目】某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
（1）这批样品的平均质量比标准质量多还是少？多或少几克？
（2）若每袋标准质量为450克，则抽样检测的总质量是多少？
【题目】有这样一个问题：探究函数y=﹣ 
+|x|的图象与性质． 小军根据学习函数的经验，对函数y=﹣ +|x|的图象与性质进行了探究．
下面是小军的探究过程，请补充完整：
（1）函数y=﹣ +|x|的自变量x的取值范围是；
（2）表是y与x的几组对应值
x | ﹣2 | ﹣1.9 | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 1 | 2 | 3 | 4 | … |
y | 2 | 1.60 | 0.80 | 0 | ﹣0.72 | ﹣1.41 | ﹣0.37 | 0 | 0.76 | 1.55 | … |
在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）观察图象，函数的最小值是；
（4）进一步探究，结合函数的图象，写出该函数的一条性质（函数最小值除外）： ．
