题目内容
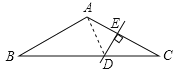
【题目】如图，在等腰△ABC中，∠BAC=120°，DE是AC的垂直平分线，DE=1cm，求BD的长．
【答案】4cm
【解析】试题分析：连接AD，先根据等腰三角形两底角相等求出∠B、∠C，根据线段垂直平分线上的点到两端点的距离相等可得AD=CD，根据等腰三角形两底角相等可得∠C=∠CAD，再求出∠BAD，然后根据直角三角形30°角所对的直角边等于斜边的一半求解即可．
试题解析：解：连接AD．∵等腰△ABC中，∠BAC=120°，∴∠B=∠C=
×（180°-120°）=30°．∵DE是AC的垂直平分线，∴AD=CD，∴∠C=∠CAD=30°，∴∠BAD=∠BAC-∠CAD=120°-30°=90°．∵DE=1cm，DE⊥AC，∴CD=2DE=2cm，∴AD=2cm．在Rt△ABD中，BD=2AD=2×2=4cm．
练习册系列答案
阅读快车系列答案
相关题目
【题目】地表以下岩层的温度T(℃)随着所处的深度h(km)的变化而变化，T与h之间在一定范围内近似地成一次函数关系．
(1)根据下表，求T(℃)与h(km)之间的函数关系式；
温度T(℃) | … | 90 | 160 | 300 | … |
深度h(km) | … | 2 | 4 | 8 | … |
(2)当岩层温度达到1770℃时，岩层所处的深度为多少？